0 319936 319944 319950 319954 319960 319962 319966 319972 319974 319980 319986 319990 319992 319996 320002 320004 320010 320014 320016 320020 320022 320026 320028 320030 320031 320032 320034 320035 320036 320038 320040 320044 320046 320050 320052 320056 320062 320064 320070 320074 320076 320080 320086 320092 320094 320100 320104 320106 320112 320116 320122 320130 366461
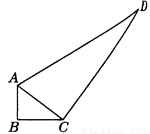
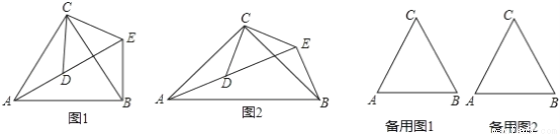
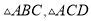 的面积.
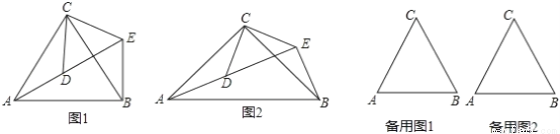
的面积. ∠B=90°,AB=3,BC=4,AC=
∠B=90°,AB=3,BC=4,AC=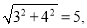
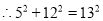 =169,
=169,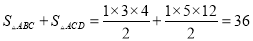 .
.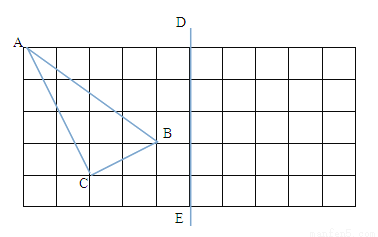
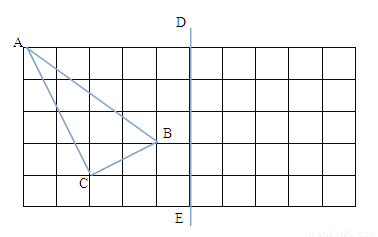
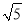 ,AB=
,AB=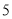 ,BC=
,BC=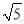 ,
, 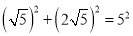 ,所以∠ACB=90°,面积等于
,所以∠ACB=90°,面积等于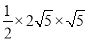 =5.
=5.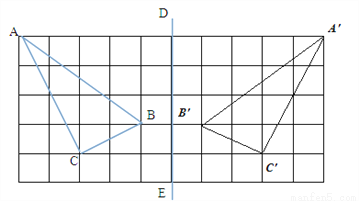
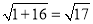 ,
,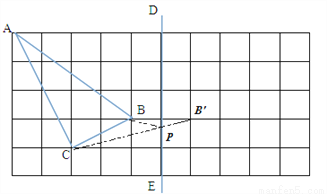
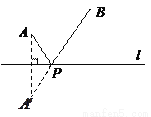
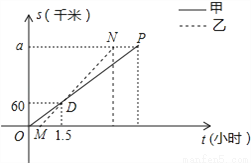
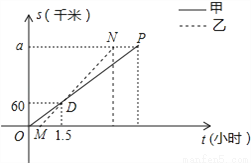
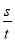 求速度.(2) ,利用v=
求速度.(2) ,利用v=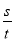 为等量列方程求解.
为等量列方程求解.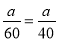 ﹣1﹣0.5,解得:a=180;
﹣1﹣0.5,解得:a=180;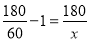 ,
,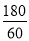 -1=2,
-1=2,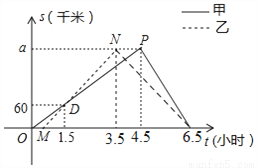
 ,
, ,
,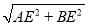 =17;
=17;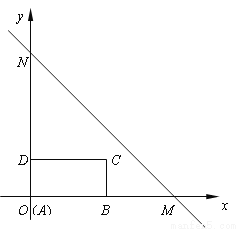
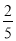 πxy2的系数为﹣
πxy2的系数为﹣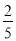 ;②1是单项式;③绝对值等于它本身的数是正数;④倒数等于它本身的数有±1;⑤
;②1是单项式;③绝对值等于它本身的数是正数;④倒数等于它本身的数有±1;⑤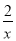 ﹣5是代数式;⑥单项式(﹣2)x2y3的次数为7.
﹣5是代数式;⑥单项式(﹣2)x2y3的次数为7.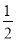 x2ym+3是同类项,则m,n的值为( )
x2ym+3是同类项,则m,n的值为( )