0 319020 319028 319034 319038 319044 319046 319050 319056 319058 319064 319070 319074 319076 319080 319086 319088 319094 319098 319100 319104 319106 319110 319112 319114 319115 319116 319118 319119 319120 319122 319124 319128 319130 319134 319136 319140 319146 319148 319154 319158 319160 319164 319170 319176 319178 319184 319188 319190 319196 319200 319206 319214 366461
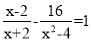 .
.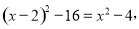
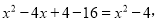
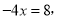
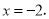
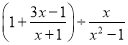 ,其中x是不等式组
,其中x是不等式组 的整数解.
的整数解.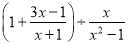 ,其中x是不等式组
,其中x是不等式组 的整数解.
的整数解.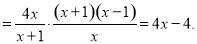
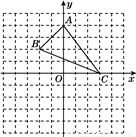
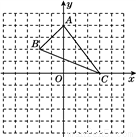
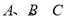 关于
关于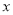 轴的对称点
轴的对称点 的位置,然后顺次连接即可;
的位置,然后顺次连接即可;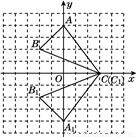
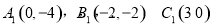
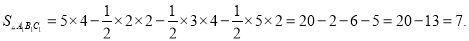
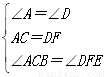 ,
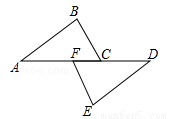
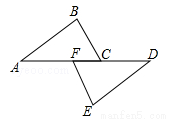
,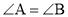 ,AE=BD,点D在AC边上,
,AE=BD,点D在AC边上,  ,AE和BD相交于点O.
,AE和BD相交于点O.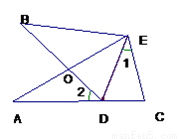
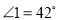 ,求?BDE的度数.
,求?BDE的度数.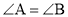 ,AE=BD,点D在AC边上,
,AE=BD,点D在AC边上, 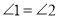 ,AE和BD相交于点O.
,AE和BD相交于点O.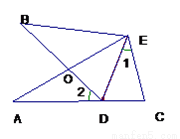
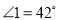 ,求?BDE的度数.
,求?BDE的度数.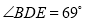 .
.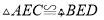
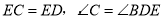 根据等腰三角形的性质即可知
根据等腰三角形的性质即可知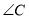 的度数,从而可求出
的度数,从而可求出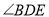 的度数;
的度数;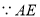 和
和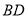 相交于点
相交于点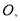
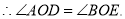
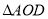 和
和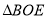 中,
中,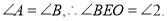
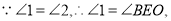
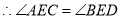 .
. 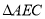 和
和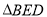 中,
中,
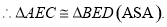
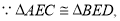
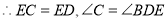 .
.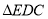 中,
中,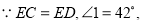
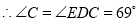 ,
,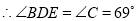 .
.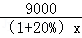 =2×
=2×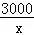 +300,
+300,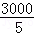 +
+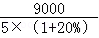 ﹣600]×9+600×9×80%﹣(3000+9000)
﹣600]×9+600×9×80%﹣(3000+9000)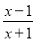 ,
, 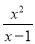 ;当分子的次数小于分母的次数时,我们称之为“真分式”,例如:
;当分子的次数小于分母的次数时,我们称之为“真分式”,例如: 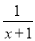 ,
, 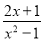 .我们知道,假分数可以化为带分数,例如:
.我们知道,假分数可以化为带分数,例如: 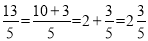 ,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如:
,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如: 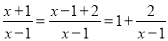 .
.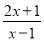 化为带分式;
化为带分式;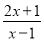 的值也是整数?
的值也是整数?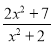 的最大值为 .
的最大值为 .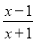 ,
, 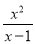 ;当分子的次数小于分母的次数时,我们称之为“真分式”,例如:
;当分子的次数小于分母的次数时,我们称之为“真分式”,例如: 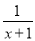 ,
, 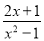 .我们知道,假分数可以化为带分数,例如:
.我们知道,假分数可以化为带分数,例如: 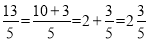 ,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如:
,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如: 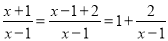 .
.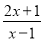 化为带分式;
化为带分式;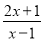 的值也是整数?
的值也是整数?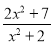 的最大值为 .
的最大值为 .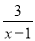 ;(2)x=0,2,﹣2,4;(3)
;(2)x=0,2,﹣2,4;(3)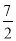 .
.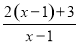 =2+
=2+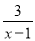 ;
;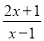 =2+
=2+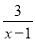 ,
,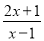 为整数,则
为整数,则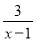 必为整数,
必为整数,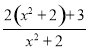 =2+
=2+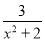 ,
,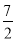 .
.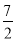 .
.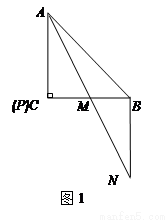
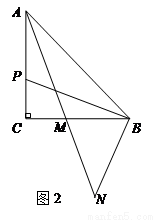
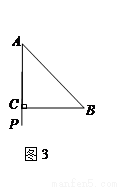
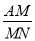 =______,
=______,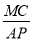 =______.(直接写出结果)
=______.(直接写出结果)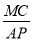 =______.
=______.