10.某厂一周计划生产700个零件,平均每天生产100个,由于各种原因实际每天生产量与计划量相比有出入,如表是某周每天的生产情况(超产为正,减产为负.单位:个)
该厂实行计件工资制,每生产一个零件10元,若当天超额完成任务,当天超出部分每个15元,若当天完不成任务当天生产出的零件每个只能按5元发工资,那么该厂工人这一周的工资总额是多少?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +2 | -3 | -1 | +8 | -7 | +10 | -5 |
5.用平面去截五棱柱,在所得的截面中,不可能出现的是( )
| A. | 八边形 | B. | 四边形 | C. | 六边形 | D. | 三角形 |
4.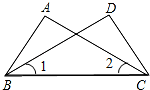 如图,已知∠ABC=∠DCB,下列条件中不能使△ABC≌△DCB的是( )
如图,已知∠ABC=∠DCB,下列条件中不能使△ABC≌△DCB的是( )
 如图,已知∠ABC=∠DCB,下列条件中不能使△ABC≌△DCB的是( )
如图,已知∠ABC=∠DCB,下列条件中不能使△ABC≌△DCB的是( )| A. | AB=DC | B. | AC=DB | C. | ∠1=∠2 | D. | ∠A=∠D |
3.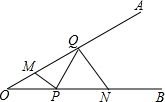 如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P、Q分别是边OB,OA上的动点,记∠AMP=∠1,∠ONQ=∠2,当MP+PQ+QN最小时,则关于∠1,∠2的数量关系正确的是( )
如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P、Q分别是边OB,OA上的动点,记∠AMP=∠1,∠ONQ=∠2,当MP+PQ+QN最小时,则关于∠1,∠2的数量关系正确的是( )
 如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P、Q分别是边OB,OA上的动点,记∠AMP=∠1,∠ONQ=∠2,当MP+PQ+QN最小时,则关于∠1,∠2的数量关系正确的是( )
如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P、Q分别是边OB,OA上的动点,记∠AMP=∠1,∠ONQ=∠2,当MP+PQ+QN最小时,则关于∠1,∠2的数量关系正确的是( )| A. | ∠1+∠2=90° | B. | 2∠2-∠1=30° | C. | 2∠1+∠2=180° | D. | ∠1-∠2=90° |
1.某商店新进货10箱水果,以每箱15千克为标准(不含纸箱重量),超过或不足的千克数分别用正、负数来表示,依据每箱差值大小依次记为A、B、C、D、E五类,见下表:
(1)10箱水果中,最重的一箱比最轻的一箱多4.5千克;
(2)这10箱水果的总重量是153千克;
(3)这批水果有两种销售方式:
甲种:每箱60元;
乙种:按每箱中的水果实际重量计算,每千克4元;
王老师从A、B、D、E四类水果中选择了若干箱,发现用甲种方式购买比用乙种方式购买节约16元,试求王老师各类水果各类水果各购买了几箱(要求写出所有可能)?
0 311071 311079 311085 311089 311095 311097 311101 311107 311109 311115 311121 311125 311127 311131 311137 311139 311145 311149 311151 311155 311157 311161 311163 311165 311166 311167 311169 311170 311171 311173 311175 311179 311181 311185 311187 311191 311197 311199 311205 311209 311211 311215 311221 311227 311229 311235 311239 311241 311247 311251 311257 311265 366461
| 水果箱的类别 | A | B | C | D | E |
| 与标准质量的差值(单位:千克) | -2 | -1.5 | 0 | 1 | 2.5 |
| 箱数 | 1 | 3 | 1 | 2 | 3 |
(2)这10箱水果的总重量是153千克;
(3)这批水果有两种销售方式:
甲种:每箱60元;
乙种:按每箱中的水果实际重量计算,每千克4元;
王老师从A、B、D、E四类水果中选择了若干箱,发现用甲种方式购买比用乙种方式购买节约16元,试求王老师各类水果各类水果各购买了几箱(要求写出所有可能)?
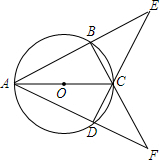 如图,四边形ABCD内接于⊙O,AB与DC的延长线交于点E,AD与BC的延长线交于点F.若∠E=∠F=44°.
如图,四边形ABCD内接于⊙O,AB与DC的延长线交于点E,AD与BC的延长线交于点F.若∠E=∠F=44°. 如图,△ABC是边长为2的等边三角形,O是BC边的中点,D、E分别在AB、AC上,∠DOE=120°,求BD+CE的长.
如图,△ABC是边长为2的等边三角形,O是BC边的中点,D、E分别在AB、AC上,∠DOE=120°,求BD+CE的长.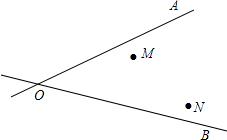 某地有两个村庄M、N和两条相交叉的公路OA,OB,现计划修建一个物资仓库,希望仓库到两个村庄的距离相等,到两条公路的距离也相等,请你用尺规作图的方法确定该点P.(注意保留作图痕迹,不用写作法)
某地有两个村庄M、N和两条相交叉的公路OA,OB,现计划修建一个物资仓库,希望仓库到两个村庄的距离相等,到两条公路的距离也相等,请你用尺规作图的方法确定该点P.(注意保留作图痕迹,不用写作法)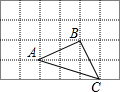 如图是单位长度为1的正方形网格,点A、B、C都在格点上;
如图是单位长度为1的正方形网格,点A、B、C都在格点上;