

 操作:
操作: 小英准备制作一个表面积为6cm2的正方体纸盒,现选用一些废弃的纸片进行如下设计:
小英准备制作一个表面积为6cm2的正方体纸盒,现选用一些废弃的纸片进行如下设计:
 | |||
 | |||

纸片利用率=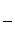 ×100%
×100%
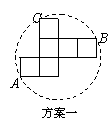
发现:(1) 小英发现方案一中的点A.B恰好为该圆一直径的两个端点.你认为
小英发现方案一中的点A.B恰好为该圆一直径的两个端点.你认为 小英的这个发现是否正确,请说明理由.
小英的这个发现是否正确,请说明理由.
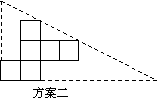
(2) 小英通过计算,发现方案一中纸片的利用率仅约为38.2%.请帮忙计算方案二的利用率,并写
小英通过计算,发现方案一中纸片的利用率仅约为38.2%.请帮忙计算方案二的利用率,并写 出求解过程.(结果精确到0.1%)
出求解过程.(结果精确到0.1%)
|
 小英感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.(结果精确到0.1%)
小英感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.(结果精确到0.1%) 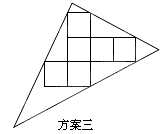
某股份有限公司根据公司实际情况,对本公司职工实行内部医疗公积金制度,公司规定:
(一)每位职工在年初需缴纳医疗公积金m元;
(二)职工个人当年治病花费的医疗费年底按表1的办法分段处理:
表1
| 分段方式 | 处理办法 |
| 不超过150元(含150元) | 全部由个人承担 |
| 超过150元,不超过10000元(不含150元,含10000元)的部分 | 个人承担n%,剩余部分由公司承担 |
| 超过10000元(不含10000元)的部分 | 全部由公司承担 |
设一职工当年治病花费的医疗费为x元,他个人实际承担的费用(包括医疗费个人承担的部分和缴纳的医疗公积金m元)为y元.
(1)由表1可知,当 时,
时, ;那么,当
;那么,当 时,y = ▲ ;
时,y = ▲ ;
(用含m、n、x的方式表示)
(2)该公司职工小红和大明2014年治病花费的医疗费和他们个人实际承担的费用如表2:
| 职工 | 治病花费的医疗费x(元) | 个人实际承担的费用y(元) |
| 小红 | 300 | 280 |
| 大明 | 500 | 320 |
请根据表2中的信息,求m、n的值,并求出当 时,y关于x函数解析式;
时,y关于x函数解析式;
(3)该公司职工个人一年因病实际承担的费用最多只需要多少元?
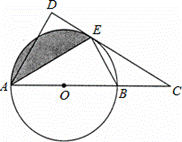
如图 ,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.
,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.
(1)求证:AE平分∠DAC;
(2)若AB=6 ,∠ABE=60°.
,∠ABE=60°.
①求AD的长; ②求出图中阴影部分的面积.

 迹,不写作法)
迹,不写作法)
 的解集.
的解集.