一组数据：1，4，2，5，3的中位数是         ．

使式子有意义的x的取值范围是      ．

如图，水平线l₁∥l₂，铅垂线l₃∥l₄，l₁⊥l₃，若选择l₁、l₂其中一条当成x轴，且向右为正方向，再选择l₃、l₄其中一条当成y轴，且向上为正方向，并在此平面直角坐标系中画出二次函数y＝ax²－ax－a的图象，则下列关于x、y轴的叙述，正确的是

不等式组的解集在数轴上表示正确的是

如图，∠1＝50°，如果AB∥DE，那么∠D＝

A．40°                         B．50°                                              C． 130°                                       D．140°

南京青奥会期间约有1020000人次参与了青奥文化教育活动．将数据1020000用科学记数法表示为

 　　　　A．10.2×10⁵B．1.02×10⁵    C．1.02×10⁶                               D．1.02×10⁷

等于

A．－3                         B．3                                                        C．±3                                                 D．

2的相反数是

A．－2                         B．－                                             C．                                                    D．2

如图1，对于平面上小于等于的，我们给出如下定义：若点P在

的内部或边上，作于点E，于点，则将称为点

P与的“点角距”，记作d(∠MON，P)．如图2，在平面直角坐标系xoy中，

x、y正半轴所组成的角为∠xOy．

（1）已知点A（5，0）、点B（3，2），则d(∠xOy，A) ＝       ，d(∠xOy，B) ＝       ．

（2）若点P为∠xOy内部或边上的动点，且满足d(∠xOy，P)＝5，画出点P运动所

形成的图形．

       （3）如图3与图4，在平面直角坐标系xoy中，射线OT的函数关系式为y＝x（x≥0）．

①在图3中，点C的坐标为（4，1），试求d(∠xOT，C)的值；

②在图4中，抛物线y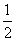＝－x ²＋2x＋ 经过A（5，0）与点D(3，4)两点，点Q是A，D两点之间的抛物线上的动点（点Q可与A，D两点重合），求当d(∠xOT，Q)取最大值时点Q 的坐标．

如图①，梯形ABCD中，AD∥BC，∠C＝90°，BA＝BC．动点E、F同时从

点B出发，点E沿折线 BA–AD–DC运动到点C时停止运动，点F沿BC运动到点

C时停止运动，它们运动时的速度都是1 cm/s．设E出发t s时，△EBF的面积为y cm²．已

知y与t的函数图象如图②所示，其中曲线OM为抛物线的一部分，MN、NP为线段．

请根据图中的信息，解答下列问题：

   （1）AD＝     cm，BC＝     cm；

   （2）求a的值，并用文字说明点N所表示的实际意义；