点M（a，﹣5）与点N（﹣2，b）关于x轴对称，则a+b=　_________　．

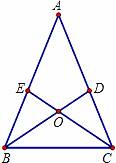
如图，在△ABC中，AB=AC，∠ABC、∠ACB的平分线BD，CE相交于O点，且BD交AC于点D，CE交AB于点E．某同学分析图形后得出以下结论：①△BCD≌△CBE；②△BAD≌△BCD；③△BDA≌△CEA；④△BOE≌△COD；⑤△ACE≌△BCE；上述结论一定正确的是（　　）

要测量河两岸相对的两点A，B的距离，先在AB的垂线BF上取两点C，D，使CD=BC，再定出BF的垂线DE，使A，C，E在一条直线上（如图所示），可以说明△EDC≌△ABC，得ED=AB，因此测得ED的长就是AB的长，判定△EDC≌△ABC最恰当的理由是（　　）

．如图，点B、C、E在同一条直线上，△ABC与△CDE都是等边三角形，则下列结论不一定成立的是（　　）

如图，在△ABC和△A′B′C′中，AB=A′B′，∠B=∠B′，补充条件后仍不一定能保证△ABC≌△A′B′C′，则补充的这个条件是（　　）

如图，a、b、c分别表示△ABC的三边长，则下面与△ABC一定全等的三角形是（　　）

下列图形中对称轴最多的是（　　）

点M（1，2）关于y轴对称点的坐标为（　　）

将一张长方形纸片只折一次，使得折痕平分这个长方形的面积，这样的方法共有（　　）

已知等腰三角形的两边长分别是3和6，则它的周长等于（　　）