阅读下列材料并填空.
平面上有n个点(n≥2)且任意三个点不在同一条直线上,过其中的每两点画直线,一共能作出多少条不同的直线?
①分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线…
②归纳:考察点的个数和可连成直线的条数Sn发现:如下表
| 点的个数 | 可作出直线条数 |
| 2 | 1=S2=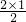 |
| 3 | 3=S3= |
| 4 | 6=S4= |
| 5 | 10=S5= |
| … | … |
| n | Sn= |
 ④结论:Sn=
④结论:Sn= 试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?(1)分析:
当仅有3个点时,可作出______个三角形;
当仅有4个点时,可作出______个三角形;
当仅有5个点时,可作出______个三角形;
…
(2)归纳:考察点的个数n和可作出的三角形的个数Sn,发现:(填下表)
| 点的个数 | 可连成三角形个数 |
| 3 | |
| 4 | |
| 5 | |
| … | |
| n |
(4)结论:
 -sin30°
-sin30°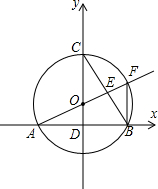 如图,O为圆心,交坐标轴于x、y轴,延长AO至F,交BC于E.OD=1,∠AOD=60°,连接FB.则下列结论不正确的是
如图,O为圆心,交坐标轴于x、y轴,延长AO至F,交BC于E.OD=1,∠AOD=60°,连接FB.则下列结论不正确的是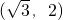

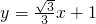

 如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,EF∥AB,交AD于点F.
如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,EF∥AB,交AD于点F. 已知如图,四边形ABCD为平行四边形,AD=a,AC为对角线,BM∥AC,过点D作 DE∥CM,交AC的延长线于F,交BM的延长线于E.
已知如图,四边形ABCD为平行四边形,AD=a,AC为对角线,BM∥AC,过点D作 DE∥CM,交AC的延长线于F,交BM的延长线于E. 如图,AB是⊙O的直径,C、D、E都是⊙O上的点,则∠1+∠2=________.
如图,AB是⊙O的直径,C、D、E都是⊙O上的点,则∠1+∠2=________.