如图，C是AB的中点，AD=BE，CD=CE．
如图，在△ABC中，AB=AC，∠B=60°，∠FAC、∠ECA是△ABC的两个外角，AD平分∠FAC，CD平分∠ECA．
在Rt△ABC中，∠C=90°，AC=1，BC=
，点O为Rt△ABC内一点，连接A0、BO、CO，且∠AOC=∠COB=BOA=120°，按下列要求画图（保留画图痕迹）：
用水平线和竖起线将平面分成若干个边长为1的小正方形格子，小正方形的顶点称为格点，以格点为顶点的多边形称为格点多边形．设格点多边形的面积为S，该多边形各边上的格点个数和为a，内部的格点个数为b，则S=
a+b-1（史称“皮克公式”）．
小明认真研究了“皮克公式”，并受此启发对正三角开形网格中的类似问题进行探究：正三角形网格中每个小正三角形面积为1，小正三角形的顶点为格点，以格点为顶点的多边形称为格点多边形，下图是该正三角形格点中的两个多边形：
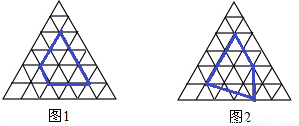
根据图中提供的信息填表：
则S与a、b之间的关系为S=______（用含a、b的代数式表示）．
0 151832 151840 151846 151850 151856 151858 151862 151868 151870 151876 151882 151886 151888 151892 151898 151900 151906 151910 151912 151916 151918 151922 151924 151926 151927 151928 151930 151931 151932 151934 151936 151940 151942 151946 151948 151952 151958 151960 151966 151970 151972 151976 151982 151988 151990 151996 152000 152002 152008 152012 152018 152026 366461
a+b-1（史称“皮克公式”）．小明认真研究了“皮克公式”，并受此启发对正三角开形网格中的类似问题进行探究：正三角形网格中每个小正三角形面积为1，小正三角形的顶点为格点，以格点为顶点的多边形称为格点多边形，下图是该正三角形格点中的两个多边形：
根据图中提供的信息填表：
| 格点多边形各边上的格点的个数 | 格点边多边形内部的格点个数 | 格点多边形的面积 | |
| 多边形1 | 8 | 1 | |
| 多边形2 | 7 | 3 | |
| … | … | … | … |
| 一般格点多边形 | a | b | S |
在平面直角坐标系xOy中，一次函数y=2x+2的图象与x轴交于A，与y轴交于点C，点B的坐标为（a，0），（其中a＞0），直线l过动点M（0，m）（0＜m＜2），且与x轴平行，并与直线AC、BC分别相交于点D、E，P点在y轴上（P点异于C点）满足PE=CE，直线PD与x轴交于点Q，连接PA．
