春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.九(1)班数学建模兴趣小组根据调查,整理出第x天(1≤x≤20且x为整数)的捕捞与销售的相关信息如表:
(1)在此期间该养殖场每天的捕捞量与前一天末的捕捞量相比是如何变化的?
(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第x天的收入y(元)与x(天)之间的函数关系式?(当天收入=日销售额-日捕捞成本)
(3)试说明(2)中的函数y随x的变化情况,并指出在第几天y取得最大值,最大值是多少?
| 鲜鱼销售单价(元/kg) | 20 |
| 单位捕捞成本(元/kg) | 5-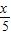 |
| 捕捞量(kg) | 950-10x |
(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第x天的收入y(元)与x(天)之间的函数关系式?(当天收入=日销售额-日捕捞成本)
(3)试说明(2)中的函数y随x的变化情况,并指出在第几天y取得最大值,最大值是多少?
面对国际金融危机.某铁路旅行社为吸引市民组团去某风景区旅游,现推出如下标准:某单位组织员工去该风景区旅游,设有x人参加,应付旅游费y元.
(1)请写出y与x的函数关系式;
(2)若该单位现有45人,本次旅游至少去26人,则该单位最多应付旅游费多少元?
0 126518 126526 126532 126536 126542 126544 126548 126554 126556 126562 126568 126572 126574 126578 126584 126586 126592 126596 126598 126602 126604 126608 126610 126612 126613 126614 126616 126617 126618 126620 126622 126626 126628 126632 126634 126638 126644 126646 126652 126656 126658 126662 126668 126674 126676 126682 126686 126688 126694 126698 126704 126712 366461
(1)请写出y与x的函数关系式;
(2)若该单位现有45人,本次旅游至少去26人,则该单位最多应付旅游费多少元?
| 人数 | 不超过25人 | 超过25人但不超过50人 | 超过50人 |
| 人均旅游费 | 1500元 | 每增加1人,人均旅游费降低20元 | 1000元 |
 x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元)(利润=销售额-成本-广告费).
x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元)(利润=销售额-成本-广告费). x2元的附加费,设月利润为w外(元)(利润=销售额-成本-附加费).
x2元的附加费,设月利润为w外(元)(利润=销售额-成本-附加费). ).
). 的五边形中结的矩形MGCH,M必须在线段EF上.
的五边形中结的矩形MGCH,M必须在线段EF上.
