0 113716 113724 113730 113734 113740 113742 113746 113752 113754 113760 113766 113770 113772 113776 113782 113784 113790 113794 113796 113800 113802 113806 113808 113810 113811 113812 113814 113815 113816 113818 113820 113824 113826 113830 113832 113836 113842 113844 113850 113854 113856 113860 113866 113872 113874 113880 113884 113886 113892 113896 113902 113910 366461
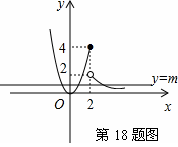 【解答】分段函数y=
【解答】分段函数y=