某公司有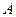 型产品40件,
型产品40件,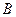 型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
(1)设分配给甲店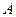 型产品
型产品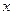 件,这家公司卖出这100件产品的总利润为
件,这家公司卖出这100件产品的总利润为 (元),求
(元),求 关于
关于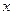 的函数关系式,并求出
的函数关系式,并求出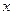 的取值范围;
的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店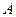 型产品让利销售,每件让利
型产品让利销售,每件让利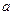 元,但让利后
元,但让利后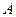 型产品的每件利润仍高于甲店
型产品的每件利润仍高于甲店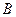 型产品的每件利润.甲店的
型产品的每件利润.甲店的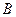 型产品以及乙店的
型产品以及乙店的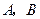 型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
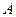 型产品40件,
型产品40件,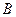 型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:| | 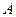 型利润 型利润 | 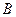 型利润 型利润 |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
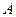 型产品
型产品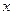 件,这家公司卖出这100件产品的总利润为
件,这家公司卖出这100件产品的总利润为 (元),求
(元),求 关于
关于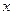 的函数关系式,并求出
的函数关系式,并求出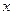 的取值范围;
的取值范围;(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店
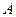 型产品让利销售,每件让利
型产品让利销售,每件让利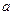 元,但让利后
元,但让利后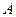 型产品的每件利润仍高于甲店
型产品的每件利润仍高于甲店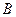 型产品的每件利润.甲店的
型产品的每件利润.甲店的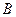 型产品以及乙店的
型产品以及乙店的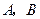 型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
下列运算中,正确的是
A.x x x = = | B. x+x =x =x | C. 2x ÷x ÷x ="x" ="x" | D.( ) ) = = |
若 在实数范围内有意义,则x的取值范围是( )
在实数范围内有意义,则x的取值范围是( )
0 113080 113088 113094 113098 113104 113106 113110 113116 113118 113124 113130 113134 113136 113140 113146 113148 113154 113158 113160 113164 113166 113170 113172 113174 113175 113176 113178 113179 113180 113182 113184 113188 113190 113194 113196 113200 113206 113208 113214 113218 113220 113224 113230 113236 113238 113244 113248 113250 113256 113260 113266 113274 366461
 在实数范围内有意义,则x的取值范围是( )
在实数范围内有意义,则x的取值范围是( )| A. x≥-2 | B. x≠-2 | C. x≥2 | D. x≠2 |
 ;
; 
 中,
中, ,
, ,将
,将 绕点
绕点 沿逆时针方向旋转
沿逆时针方向旋转 得到
得到 .
.
 的长是 ,
的长是 , 的度数是 ;
的度数是 ; ,求证:四边形
,求证:四边形 是平行四边形;
是平行四边形; ,∠C=60°,求斜坡AB、CD的长。
,∠C=60°,求斜坡AB、CD的长。

 ,则线段BC上是否存在一点P,使得以P,D,B为顶点的三角形与△BCO相似.若存在,求出DP的长;若不存在,请说明理由.
,则线段BC上是否存在一点P,使得以P,D,B为顶点的三角形与△BCO相似.若存在,求出DP的长;若不存在,请说明理由. ,其中
,其中 .如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边
.如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边 交于点
交于点 ,与边
,与边 交于点
交于点 .
.
 与点
与点 重合,求点
重合,求点 上的点为
上的点为 ,设
,设 ,
, ,试写出
,试写出 关于
关于 的函数解析式,并确定
的函数解析式,并确定 ,求此时点
,求此时点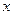 轴交于点
轴交于点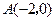 ,
,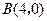 ,与
,与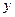 轴交于点
轴交于点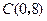 .
.
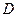 的坐标;
的坐标;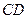 交
交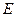 .在线段
.在线段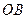 的垂直平分线上是否存在点
的垂直平分线上是否存在点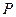 ,使得点
,使得点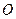 的距离?如果存在,求出点
的距离?如果存在,求出点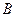 作
作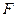 ,将抛物线沿其对称轴平移,使抛物线与线段
,将抛物线沿其对称轴平移,使抛物线与线段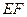 总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?