开始向点C以每秒0.25cm的速度运动, 当点P运动到PA与腰垂直的位置时，点P运动的时间应为__ _____秒.
（6分）十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F
）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单多面体模型，解答下列问题：
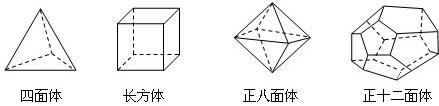
【小题1】（1）根据上面多面体模型，完成表格中的空格：
【小题2】（2）你发现顶点数（V）、面数（F）、棱数（E）之间存在的关系式是
【小题3】（3）一个多面体的面数比顶点数大8，且有30条棱，则这个多面体的面数是
【小题4】（4）某个玻璃鉓品的外形是简单多面体，它的外表面是由三角形和八边形两种多边形拼接而成，且有24个顶点，每个顶点处都有3条棱，设该多面体外表三角形的个数为x个，八边形的个数为y个，x+y=
）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单多面体模型，解答下列问题：【小题1】（1）根据上面多面体模型，完成表格中的空格：
| 多面体 | 顶点数（V） | 面数（F） | 棱数（E） |
| 四面体 | 4 | 4 | 6 |
| 长方体 | 8 | 6 | 12 |
| 正八面体 | 6 | 8 | 12 |
| 正十二面体 | | | |
【小题3】（3）一个多面体的面数比顶点数大8，且有30条棱，则这个多面体的面数是
【小题4】（4）某个玻璃鉓品的外形是简单多面体，它的外表面是由三角形和八边形两种多边形拼接而成，且有24个顶点，每个顶点处都有3条棱，设该多面体外表三角形的个数为x个，八边形的个数为y个，x+y=
（6分）：某学校举行演讲比赛，选出了10名同学担任评委，并事先拟定从以下4个方案中选择合理的方案来确定每个演讲者的最后得分。
方案1：所有评委所给分的平均数．方案2：在所有评委所给分中，去掉一个最高分和一个最低分，然后再计算其余给分的平均数．
方案3：所有评委所给分的中位数．
方案4：所有评委所给分的众数．
为了探究上述方案的合理性，先对某个同学的演讲成绩进行了统计实验．下面是这个同学的得分统计图：
【小题1】（1）分别按上述4个方案计算这个同学演讲的最后得分；
【小题2】（2）根据（1）中的结果，请用统计的知识说明哪些方案不适合作为这个同学演讲的最后得分．
0 110910 110918 110924 110928 110934 110936 110940 110946 110948 110954 110960 110964 110966 110970 110976 110978 110984 110988 110990 110994 110996 111000 111002 111004 111005 111006 111008 111009 111010 111012 111014 111018 111020 111024 111026 111030 111036 111038 111044 111048 111050 111054 111060 111066 111068 111074 111078 111080 111086 111090 111096 111104 366461
方案1：所有评委所给分的平均数．方案2：在所有评委所给分中，去掉一个最高分和一个最低分，然后再计算其余给分的平均数．
方案3：所有评委所给分的中位数．
方案4：所有评委所给分的众数．
|
【小题1】（1）分别按上述4个方案计算这个同学演讲的最后得分；
【小题2】（2）根据（1）中的结果，请用统计的知识说明哪些方案不适合作为这个同学演讲的最后得分．
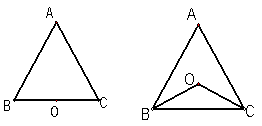
的坐标为（2，0），请在图中分别标明B(5,3)、C(-2,5) 关于直线l的对称点
、
的位置，并写出他们的坐标: 
的坐标为 
，y）从M（1，0）出发，沿由A（-1，1），B（-1，-1），C（1，-1），D（1，1）四点组成的正方形边线（如图①）按一定方向运动。图②是P点运动的路程s（个单位）与运动时间
（秒）之间的函数图象，图③是P点的纵坐标y与P点运动的路程s之间的函数图象的一部分.
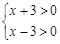（2）
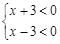
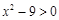的解集为x﹥3或x﹤-3.