题目内容

 三角形的三边为a、b、c，由下列条件不能判断它是直角三角形的是（     ）

A．a:b:c=8∶16∶17     B． a2-b2=c2     C．a2=(b+c)(b-c)     D． a=26  b=10  c=24

A

详细解答: A．a:b:c=8∶16∶17，可设a＝8k，b＝16k，c＝17k，

a2＋b2＝64k2＋256k2＝320k2，c2＝(17k)2＝289k2，

所以，a2＋b2≠c2，这个三角形不是直角三角形．

  B． a2-b2=c2  即a2 =c2+b2，这个三角形是直角三角形．

C．a2=(b+c)(b-c) 即a2 =b2-c2，所以a2 +c2= b2，这个三角形是直角三角形．

D． a=26，b=10，c=24，那么c2+b2=102+242=676，a2 =262=676，所以a2=c2+b2，这个三角形是直角三角形．

练习册系列答案
相关题目
三角形的三边为a，b，c，若b=10，a，c为整数且a≤b≤c，则该三角形是等边三角形的概率是
 
．
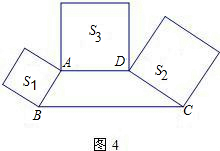精英家教网（一）小明在玩积木游戏时，把三个正方形积木摆成一定的形状，正视图如图①，
问题（1）：若此中的三角形△DEF为直角三角形，P的面积为9，Q的面积为15，则M的面积为
 
．
问题（2）：若P的面积为36cm2，Q的面积为64 cm2，同时M的面积为100 cm2，则△DEF为
 
三角形．
（二）图形变化：
Ⅰ如图②，分别以直角三角形的三边为直径向三角形外作三个半圆，你能找出这三个半圆的面积之间有什么关系吗？请说明理由．
Ⅱ如图③，如果直角三角形两直角边的长分别为3和4，以直角三角形的三边为直径作半圆，你能利用上面中的结论求出阴影部分的面积吗？
勾股定理有着悠久的历史，它曾引起很多人的兴趣．1955年希腊发行了二枚以勾股图为背景的邮票．所谓勾股图是指以直角三角形的三边为边向外作正方形构成（图1：△ABC中，∠BAC=90°）．
请解答：
（1）如图2，若以直角三角形的三边为边向外作等边三角形，则它们的面积S1、S2、S3之间的数量关系是
 
．
（2）如图3，若以直角三角形的三边为直径向外作半圆，则它们的面积S1、S2、S3之间的数量关系是
 
，请说明理由．
精英家教网
（3）如图4，在梯形ABCD中，AD∥BC，∠ABC+∠BCD=90°，BC=2AD，分别以AB、CD、AD为边向精英家教网梯形外作正方形，其面积分别为S1、S2、S3，则S1、S2、S3之间的数量关系式为
 
，请说明理由．
10、一个直角三角形的三边为三个连续偶数，则它的三边长分别为
6，8，10
．
（2012•新疆）如图所示，分别以直角三角形的三边为直径作半圆，其中两个半圆的面积S1=
25
8
π，S2=2π，则S3是
9π
8
9π
8
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网