题目内容
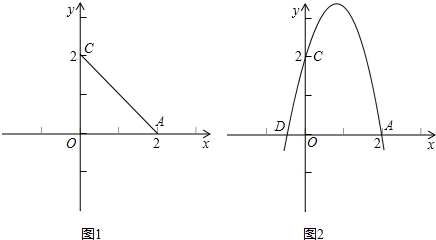
 (2012•新疆)如图所示,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积S1=
(2012•新疆)如图所示,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积S1=| 25 |
| 8 |
| 9π |
| 8 |
| 9π |
| 8 |
分析:在直角三角形中,利用勾股定理得到a2+b2=c2,在等式两边同时乘以
,变形后得到S2+S3=S1,将已知的S1与S2代入,即可求出S3的值.
| π |
| 8 |
解答: 解:在直角三角形中,利用勾股定理得:a2+b2=c2,
解:在直角三角形中,利用勾股定理得:a2+b2=c2,
∴
a2+
b2=
c2,
变形为:
(
)2π+
(
)2π=
(
)2π,即S2+S3=S1,
又S1=
,S2=2π,
则S3=S1-S2=
-2π=
.
故答案为:
 解:在直角三角形中,利用勾股定理得:a2+b2=c2,
解:在直角三角形中,利用勾股定理得:a2+b2=c2,∴
| π |
| 8 |
| π |
| 8 |
| π |
| 8 |
变形为:
| 1 |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
| b |
| 2 |
| 1 |
| 2 |
| c |
| 2 |
又S1=
| 25π |
| 8 |
则S3=S1-S2=
| 25π |
| 8 |
| 9π |
| 8 |
故答案为:
| 9π |
| 8 |
点评:此题考查了勾股定理,以及圆的面积求法,利用了转化的思想,灵活运用勾股定理是解本题的关键.

练习册系列答案
相关题目
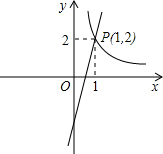 (2012•新疆)如图,一次函数y=kx-3的图象与反比例函数
(2012•新疆)如图,一次函数y=kx-3的图象与反比例函数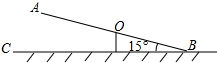 (2012•新疆)如图,跷跷板AB的一端B碰到地面时,AB与地面的夹角为15°,且OA=OB=3m.
(2012•新疆)如图,跷跷板AB的一端B碰到地面时,AB与地面的夹角为15°,且OA=OB=3m. (2012•新疆)如图,圆内接四边形ABDC,AB是⊙O的直径,OD⊥BC于E.
(2012•新疆)如图,圆内接四边形ABDC,AB是⊙O的直径,OD⊥BC于E.