Question

【题目】将纸片沿折叠，其中．

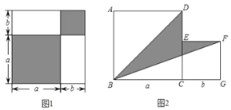
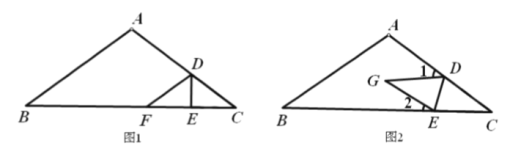
（1）如图1，点落在边上的点处，与是否平行？请说明理由；

（2）如图2，点落在四边形内部的点处，探索与之间的数量关系，并说明理由．

Answer 1

【答案】（1），理由见解析；（2），理由见解析

【解析】

（1）AB与DF平行．根据翻折可得出∠DFC=∠C，结合∠B=∠C即可得出∠B=∠DFC，从而证出AB∥DF；
（2）连接GC，由翻折可得出∠DGE=∠ACB，再根据三角形外角的性质得出∠1=∠DGC+∠DCG，∠2=∠EGC+∠ECG，通过角的运算即可得出∠1+∠2=2∠B．

解：（1）

∵将纸片沿折叠

∴

又∵

∴

则（同位角相等，两直线平行）

（2）连接GC，如图．

由翻折得:∠DGE=∠ACB．
∵∠1=∠DGC+∠DCG，∠2=∠EGC+∠ECG，
∴∠1+∠2=∠DGC+∠DCG+∠EGC+∠ECG=（∠DGC+∠EGC）+（∠DCG+∠ECG）=∠DGE+∠DCE=2∠ACB．
∵∠B=∠ACB，

∴∠1+∠2=2∠B．

∴