题目内容
 如图,AB、CD相交于E,CF、BF分别是∠ACD和∠ABD的平分线,它们相交于点F,若∠A+∠D=130°,则∠F=________度.
如图,AB、CD相交于E,CF、BF分别是∠ACD和∠ABD的平分线,它们相交于点F,若∠A+∠D=130°,则∠F=________度.
65
分析:由CF、BF分别是∠ACD和∠ABD的平分线,则∠1=∠2,∠3=∠4,根据三角形内角和定理得,∠A+∠1=∠3+∠F①,∠A+∠1+∠2=∠3+∠4+∠D,即∠A+2∠1=2∠3+∠D②,由①×2-②得,∠A=2∠F-∠D,即2∠F=∠A+∠D;若∠A+∠D=130°,即可得到∠F的度数.
解答: 解:如图,
解:如图,
∵CF、BF分别是∠ACD和∠ABD的平分线,
∴∠1=∠2,∠3=∠4,
在△AMC和△FMB中,∠A+∠1=∠3+∠F①,
在△AEC和△DEB中,∠A+∠1+∠2=∠3+∠4+∠D,即∠A+2∠1=2∠3+∠D②,
由①×2-②得,∠A=2∠F-∠D,即2∠F=∠A+∠D,
又∵∠A+∠D=130°,
∴2∠F=130°,
∴∠F=65°.
故答案为65°.
点评:本题考查了三角形的内角和定理:三角形的三个内角的和为180°.也考查了角平分线的性质.
分析:由CF、BF分别是∠ACD和∠ABD的平分线,则∠1=∠2,∠3=∠4,根据三角形内角和定理得,∠A+∠1=∠3+∠F①,∠A+∠1+∠2=∠3+∠4+∠D,即∠A+2∠1=2∠3+∠D②,由①×2-②得,∠A=2∠F-∠D,即2∠F=∠A+∠D;若∠A+∠D=130°,即可得到∠F的度数.
解答:
 解:如图,
解:如图,∵CF、BF分别是∠ACD和∠ABD的平分线,
∴∠1=∠2,∠3=∠4,
在△AMC和△FMB中,∠A+∠1=∠3+∠F①,
在△AEC和△DEB中,∠A+∠1+∠2=∠3+∠4+∠D,即∠A+2∠1=2∠3+∠D②,
由①×2-②得,∠A=2∠F-∠D,即2∠F=∠A+∠D,
又∵∠A+∠D=130°,
∴2∠F=130°,
∴∠F=65°.
故答案为65°.
点评:本题考查了三角形的内角和定理:三角形的三个内角的和为180°.也考查了角平分线的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
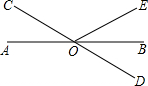 如图,AB、CD相交于点O,OB平分∠DOE,若∠DOE=60°,则∠AOC的度数是
如图,AB、CD相交于点O,OB平分∠DOE,若∠DOE=60°,则∠AOC的度数是 如图,AB与CD相交于点O,AD∥BC,AD:BC=1:3,AB=10,则AO的长是
如图,AB与CD相交于点O,AD∥BC,AD:BC=1:3,AB=10,则AO的长是 如图,AB与CD相交于点O,OA=3,OB=5,0D=6.当OC=
如图,AB与CD相交于点O,OA=3,OB=5,0D=6.当OC= (2009•同安区模拟)已知,如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点.
(2009•同安区模拟)已知,如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点. 已知:如图直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=30°.求∠2和∠3的度数.
已知:如图直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=30°.求∠2和∠3的度数.