题目内容
17.某商场统计了每个营业员在某月的销售额,统计图如下: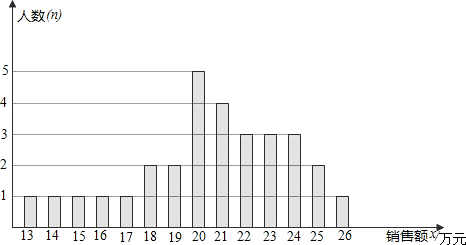
(1)设营业员的月销售额为x(单位:万元),商场规定:当x<15时为不称职,当15≤x<20时,为基本称职,当20≤x<25为称职,当x≥25时为优秀.试求出不称职、基本称职、称职、优秀四个层次营业员人数所占百分比.
(2)据(1)规定,所有称职和优秀的营业员月销售额的中位数、众数和平均数分别是多少?
(3)为了调动营业员的工作积极性,决定制定月销售额奖励标准,凡到达或超过这个标准的营业员将受到奖励.如果要使得一半称职和优秀的营业员能获奖,你认为这个奖励标准应定为多少元合适?
分析 (1)首先求出总人数与不称职、基本称职、称职、优秀四个层次营业员人数,进而求出不称职、基本称职、称职、优秀四个层次营业员人数所占百分比,再求出所占的圆心角的度数画图即可解答;
(2)根据中位数、众数和平均数的意义解答即可;
(3)如果要使得一半称职和优秀的营业员能获奖,月销售额奖励标准可以定为称职和优秀这两个层次销售额的中位数,因为中位数以上的人数占总人数的一半左右.
解答 解:(1)由图可知营业员总人数为1+1+1+1+1+2+2+5+4+3+3+3+2+1=30人;
不称职的有2人,所占百分比为 $\frac{2}{30}$×100%≈6.67%;
基本称职的有7人,所占百分比为 $\frac{7}{30}$×100%≈23.33%;
称职的有18人,所占百分比为 $\frac{18}{30}$×100%=60%;
优秀的有3人,所占百分比为 $\frac{3}{30}$×100%=10%;
(2)所有称职和优秀的营业员共21人,月销售额从小到大排列第11个数为22万元,所以22万元为中位数;
20万元出现了五次,次数最多,为众数.
平均数为:(5×20+4×21+3×22+3×23+3×24+2×25+1×26)÷21≈22.2万元;
(3)如果要使得一半称职和优秀的营业员能获奖,这个奖励标准应定为22万元合适.
因为称职和优秀的共有21人,月销售额在22万元以上(含22万元)的有12人,超过总数的一半.
点评 本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.除此之外,本题也考查了加权平均数、中位数、众数的认识.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
9.某校初三学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
经统计发现两班总数相等.此时有学生建议,可以通过考察数据中的其他信息作为参考.
请你回答下列问题:
(1)填空:甲班的优秀率为60%,乙班的优秀率为40%;
(2)填空:甲班比赛数据的中位数为100,乙班比赛数据的中位数为97;
(3)填空:估计两班比赛数据的方差较小的是甲班(填甲或乙)
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.
| 1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
| 甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
请你回答下列问题:
(1)填空:甲班的优秀率为60%,乙班的优秀率为40%;
(2)填空:甲班比赛数据的中位数为100,乙班比赛数据的中位数为97;
(3)填空:估计两班比赛数据的方差较小的是甲班(填甲或乙)
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.
6.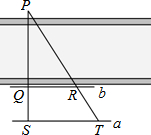 如图,为了估计河的宽度,在河的对岸选定一个目标点P,在近岸取点Q和S,使点P,Q,S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R.如果QS=60m,ST=120m,QR=80m,则河的宽度PQ为( )
如图,为了估计河的宽度,在河的对岸选定一个目标点P,在近岸取点Q和S,使点P,Q,S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R.如果QS=60m,ST=120m,QR=80m,则河的宽度PQ为( )
 如图,为了估计河的宽度,在河的对岸选定一个目标点P,在近岸取点Q和S,使点P,Q,S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R.如果QS=60m,ST=120m,QR=80m,则河的宽度PQ为( )
如图,为了估计河的宽度,在河的对岸选定一个目标点P,在近岸取点Q和S,使点P,Q,S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R.如果QS=60m,ST=120m,QR=80m,则河的宽度PQ为( )| A. | 40m | B. | 60m | C. | 120m | D. | 180m |
7.若-2amb4与5an+2b2m+n可以合并成一项,则mn的值是( )
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
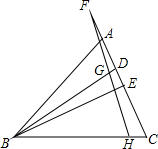 如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H;下列结论:
如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H;下列结论: