题目内容
如图AB是⊙O的直径,C是半圆上的一个三等分点,D是 的中点,P是直径AB上的一动点,⊙O的半径为1,则PC+PD的最小值为( )
的中点,P是直径AB上的一动点,⊙O的半径为1,则PC+PD的最小值为( )

A.1 B. C.
C. D.
D.
C
【解析】
试题分析:作D关于AB的对称点E,连接CE交AB于点P′,连接OC,OE,则DP+CP最小,根据解直角三角形求出CE,根据轴对称求出DP′+CP′=CE即可.
【解析】
作D关于AB的对称点E,连接CE交AB于点P′,连接OC,OE,
则根据垂径定理得:E在⊙O上,连接EC交AB于P′,则若P在P′时,DP+CP最小,
∵C是半圆上的一个三等分点,
∴∠AOC= ×180°=60°,
×180°=60°,
∵D是 的中点,
的中点,
∴∠AOE= ∠AOC=30°,
∠AOC=30°,
∴∠COE=90°,
∴CE= OC=
OC= ,
,
即DP+CP= ,
,
故选C.


练习册系列答案
相关题目
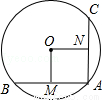


 的中点,点P是半径ON上的点.若⊙O的半径为l,则AP+BP的最小值为( )
的中点,点P是半径ON上的点.若⊙O的半径为l,则AP+BP的最小值为( )
 C.
C. D.
D.
