题目内容
19. 我们在学习三角形相似时,往往是添加平行线构造相似三角形的基本图形.有一学生根据这一理论猜想三角形内角平分线有这样一个性质:如图,在△ABC中,AD平分∠BAC,则$\frac{BD}{CD}$=$\frac{AB}{AC}$.如果你认为这个猜想是正确的,请写出一个完整的推理过程.
我们在学习三角形相似时,往往是添加平行线构造相似三角形的基本图形.有一学生根据这一理论猜想三角形内角平分线有这样一个性质:如图,在△ABC中,AD平分∠BAC,则$\frac{BD}{CD}$=$\frac{AB}{AC}$.如果你认为这个猜想是正确的,请写出一个完整的推理过程.
分析 过点D作DE∥AB交CA于点E,根据平行线分线段成比例定理得到$\frac{CD}{BD}$=$\frac{CE}{AE}$,根据平行线的性质和等腰三角形的性质得到EA=ED,得到答案.
解答 证明:过点D作DE∥AB交CA于点E,
∵DE∥AB,
∴∠EDA=∠BAD,
∵AD平分∠BAC,
∴∠BAD=∠EAD,
∴∠EDA=∠EAD,
∴EA=ED,
∵DE∥AB,
∴$\frac{CD}{BD}$=$\frac{CE}{AE}$,
∴$\frac{CD}{BD}$=$\frac{CE}{DE}$,
∵DE∥AB,
$\frac{CE}{DE}$=$\frac{CA}{AB}$,
∴$\frac{BD}{CD}$=$\frac{AB}{AC}$.
点评 本题考查的是平行线分线段成比例定理,灵活运用的、找准对应关系是解题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
10.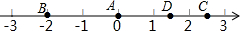 如图所示,A、B、C、D四点在数轴上分别表示有理数a、b、c、d,则大小顺序正确的是( )
如图所示,A、B、C、D四点在数轴上分别表示有理数a、b、c、d,则大小顺序正确的是( )
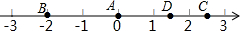 如图所示,A、B、C、D四点在数轴上分别表示有理数a、b、c、d,则大小顺序正确的是( )
如图所示,A、B、C、D四点在数轴上分别表示有理数a、b、c、d,则大小顺序正确的是( )| A. | a<b<c<d | B. | b<a<d<c | C. | a<b<d<c | D. | d<c<b<a |
11.在-$\frac{{a}^{2}}{2}$中,底数是( )
| A. | -$\frac{a}{2}$ | B. | a | C. | $\frac{a}{2}$ | D. | $\frac{1}{2}$ |
8.三角形的三边长分别为6,8,10,那它最短边上的高为( )
| A. | 4.8 | B. | 5 | C. | 6 | D. | 8 |
