题目内容
15.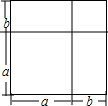 若(a+4)2+|b-1|=0,
若(a+4)2+|b-1|=0,(1)分别计算下列两个式(a+b)2与a2+2ab+b2的值,并猜想(a+b)2与a2+2ab+b2两式之间的关系.
(2)用给出的图形验证(1)中的猜想并说明理由.
(3)运用(2)中的结果计算20152-2×2015×2014+20142的值.
分析 (1)利用非负数的性质求出a与b的值,确定出两式的值,作出猜想即可;
(2)正方形面积有两种求法:直接求与间接求,即可验证猜想;
(3)利用得出的结论将原式变形,计算即可得到结果.
解答 解:(1)∵(a+4)2+|b-1|=0,
∴a=-4,b=1,
则(a+b)2=(-4+1)2=9,a2+2ab+b2=16-8+1=9,
猜想(a+b)2=a2+2ab+b2;
(2)正方形的面积为(a+b)2,还可以表示为两个正方形及两个长方形面积之和,即a2+2ab+b2,
则(a+b)2=a2+2ab+b2;
(3)原式=(2015-2014)2=1.
点评 此题考查了代数式求值,以及非负数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
7.将抛物线y=x2向上平移一个单位后,得到新的抛物线,那么新的抛物线的解析式是( )
| A. | y=x2+x | B. | y=x2-x | C. | y=x2-1 | D. | y=x2+1 |
 如图.点E是菱形ABCD边AD反向延长线上的一点,连结CE交AB于F,连结BE,过点F作FH∥AE交BE于H,求证:AF=HF.
如图.点E是菱形ABCD边AD反向延长线上的一点,连结CE交AB于F,连结BE,过点F作FH∥AE交BE于H,求证:AF=HF. 如图,正方形ABCD的边长为1,以直线AB为轴将正方形旋转一周,所得一个圆柱,求:
如图,正方形ABCD的边长为1,以直线AB为轴将正方形旋转一周,所得一个圆柱,求: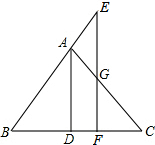 如图,在△ABC中,AD⊥BC于点D,且AD平分∠BAC,点E是BA延长线上任一点,过点E作EF⊥BC于点F,与AC交于点G.
如图,在△ABC中,AD⊥BC于点D,且AD平分∠BAC,点E是BA延长线上任一点,过点E作EF⊥BC于点F,与AC交于点G.