题目内容
3.设Pn为正n边形的周长,求正n边形的面积.分析 作OM⊥AB于M,则∠OMA=90°,由正n边形的性质得出AM=$\frac{1}{2}$AB=$\frac{{p}_{n}}{2n}$,∠AOM=$\frac{1}{2}$∠AOB=$\frac{180°}{n}$,由三角函数得出OM=$\frac{{p}_{n}}{2ntan\frac{180°}{n}}$,得出正n边形的面积=n×$\frac{1}{2}$×$\frac{{p}_{n}}{n}$×$\frac{{p}_{n}}{2ntan\frac{180°}{n}}$,即可得出结果.
解答 解:如图所示: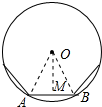
AB为正n边形的边长,
连接OA、OB,作OM⊥AB于M,
则∠OMA=90°,AM=$\frac{1}{2}$AB=$\frac{{p}_{n}}{2n}$,∠AOM=$\frac{1}{2}$∠AOB=$\frac{180°}{n}$,
∵tan$\frac{180°}{n}$=$\frac{AM}{OM}$,
∴OM=$\frac{AM}{tan\frac{180°}{n}}$=$\frac{{p}_{n}}{2ntan\frac{180°}{n}}$,
∴正n边形的面积=n×$\frac{1}{2}$×$\frac{{p}_{n}}{n}$×$\frac{{p}_{n}}{2ntan\frac{180°}{n}}$=$\frac{{{p}_{n}}^{2}}{4ntan\frac{180°}{n}}$.
点评 此题考查了正多边形与圆、正n边形的性质、三角函数;熟练掌握正n边形的性质,运用三角函数求出OM是解决问题的关键.

练习册系列答案
相关题目
8.篮球比赛平分规则是胜一场得2分,负一场得1分,白杨队共打22场比赛,得36分,则一共负了( )场.
| A. | 6场 | B. | 7场 | C. | 8场 | D. | 9场 |
18.如果一个数的绝对值等于本身,那么这个数是( )
| A. | 正数 | B. | 0 | C. | 非正数 | D. | 非负数 |
 指出下图中线段、射线、直线分别有多少条?
指出下图中线段、射线、直线分别有多少条?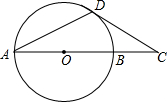 如图.AB是⊙O的直径,D是⊙O上一点,∠DAB=30°,延长AB到C,使BC=$\frac{1}{2}$AB,连接CD.求证:CD是⊙O的切线.
如图.AB是⊙O的直径,D是⊙O上一点,∠DAB=30°,延长AB到C,使BC=$\frac{1}{2}$AB,连接CD.求证:CD是⊙O的切线.