题目内容
如图所示,反比例函数 的图象经过点 A(-
的图象经过点 A(- ,b),过点A作AB垂直x轴于点B,△A
,b),过点A作AB垂直x轴于点B,△A OB的面积为
OB的面积为 .
.
(1)求k和b的值;
(2)若一次函数y=ax+1的图象经过点A,并且与x轴相交于点M,求△AOM的面积.
解:(1)点 A(- ,b),过点A作AB垂直x轴于点B,
,b),过点A作AB垂直x轴于点B,
即有OB= ,
,
又△AOB的面积为 .
.
故有 =
= ×
× b;
b;
即b=2,
A(- ,2),
,2),
代入反比例函数中,
得k=-2 ;
;
(2)将A点的坐标代入直线方程,
2= +1;
+1;
得a= ;
;
即直线方程为y=- x+1,
x+1,
令y=0,得x= ;
;
即OM= ;
;
所以S△AOM= OM•b=
OM•b= ;
;
分析:(1)根据题意,利用点A的横坐标和△AOB的面积,可得出b的值,将A的坐标代入反比函数中,即可得出k的值;
(2)将A点的坐标为代入直线方程中,可得出a的值,即得直线方程,令y=0,可得出M的坐标,即可得出OM的长,又△AOM的底边OM对应的高为点A的纵坐标,利用三角形的面积公式即可得出△AOM的面积.
点评:本题主要考查了反比例函数解析式的确定以及和一次函数的综合应用,也考查了三角形的有关知识,难度不大,属于常规性训练的试题.
 ,b),过点A作AB垂直x轴于点B,
,b),过点A作AB垂直x轴于点B,即有OB=
 ,
,又△AOB的面积为
 .
.故有
 =
= ×
× b;
b;即b=2,
A(-
 ,2),
,2),代入反比例函数中,
得k=-2
 ;
;(2)将A点的坐标代入直线方程,
2=
 +1;
+1;得a=
 ;
;即直线方程为y=-
 x+1,
x+1,令y=0,得x=
 ;
;即OM=
 ;
;所以S△AOM=
 OM•b=
OM•b= ;
;分析:(1)根据题意,利用点A的横坐标和△AOB的面积,可得出b的值,将A的坐标代入反比函数中,即可得出k的值;
(2)将A点的坐标为代入直线方程中,可得出a的值,即得直线方程,令y=0,可得出M的坐标,即可得出OM的长,又△AOM的底边OM对应的高为点A的纵坐标,利用三角形的面积公式即可得出△AOM的面积.
点评:本题主要考查了反比例函数解析式的确定以及和一次函数的综合应用,也考查了三角形的有关知识,难度不大,属于常规性训练的试题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
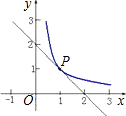 已知:如图所示,反比例函数y=
已知:如图所示,反比例函数y=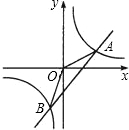 如图所示,反比例函数y=
如图所示,反比例函数y= (2013•石峰区模拟)如图所示,反比例函数
(2013•石峰区模拟)如图所示,反比例函数 二次函数y=ax2+bx+c的图象如图所示,反比例函数y=
二次函数y=ax2+bx+c的图象如图所示,反比例函数y= 如图所示,反比例函数图象上一点A,过A作AB⊥x轴于B,若S△AOB=3,则反比例函数的解析式为
如图所示,反比例函数图象上一点A,过A作AB⊥x轴于B,若S△AOB=3,则反比例函数的解析式为