题目内容
如图所示，∠AOP=∠BOP=15°，PC∥OA交OB于C，PD⊥OA于D，若PC=4，则PD等于________．
2
分析：过点P作PM⊥OB于M，根据平行线的性质可得到∠BCP的度数，再根据直角三角形的性质可求得PM的长，根据角平分线上的点到角两边的距离相等得到PM=PD，从而求得PD的长．
解答：
解：过点P作PM⊥OB于M，
∵PC∥OA，
∴∠COP=∠CPO=∠POD=15°，
∴∠BCP=30°，
∴PM=
PC=2，
∵PD=PM，
∴PD=2．
故答案为：2．
点评：本题考查了等腰三角形的性质及含30°角的直角三角形的性质；解决本题的关键就是利用角平分线的性质，把求PD的长的问题进行转化．
分析：过点P作PM⊥OB于M，根据平行线的性质可得到∠BCP的度数，再根据直角三角形的性质可求得PM的长，根据角平分线上的点到角两边的距离相等得到PM=PD，从而求得PD的长．
解答：
解：过点P作PM⊥OB于M，∵PC∥OA，
∴∠COP=∠CPO=∠POD=15°，
∴∠BCP=30°，
∴PM=
PC=2，∵PD=PM，
∴PD=2．
故答案为：2．
点评：本题考查了等腰三角形的性质及含30°角的直角三角形的性质；解决本题的关键就是利用角平分线的性质，把求PD的长的问题进行转化．
练习册系列答案
相关题目
如图所示，∠AOP=∠BOP=15°，PC∥OA交OB于C，PD⊥OA于D，若PC=4，则PD等于
如图所示，∠AOP=∠BOP=15°，PC∥OA，PD⊥OA，若PC=4，则PD等于（ ）| A、4 | B、3 | C、2 | D、1 |
9、如图所示，∠AOP=∠BOP=15°，PC∥OA，PD⊥OA，若PD=4，则PC等于（ ）
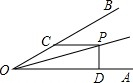如图所示，∠AOP=∠BOP=15°，PC∥OA，PD⊥OA，若PC=10，则PD等于