题目内容
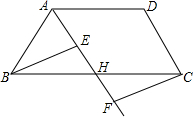 如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,使EH=FH,连接BE,CF.
如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,使EH=FH,连接BE,CF.(1)求证:△BEH≌△CFH.
(2)当BH与EH满足什么关系时,四边形BFCE是矩形?请说明理由.
考点:全等三角形的判定与性质,矩形的判定
专题:
分析:(1)求出BH=CH,根据SAS推出两三角形全等即可;
(2)根据平行四边形的判定得出四边形是平行四边形,求出BC=EF,根据矩形的判定得出即可.
(2)根据平行四边形的判定得出四边形是平行四边形,求出BC=EF,根据矩形的判定得出即可.
解答:(1)证明:∵点H是BC的中点,
∴BH=CH,
在△BEH和△CFH中
∴△BEH≌△CFH;
(2)解:当BH=EH时,四边形BFCE是矩形,
理由是:∵BH=CH,EH=FH,
∴四边形BFCE是平行四边形,
∵BH=CH,EH=FH,BH=EH,
∴BC=EF,
∴四边形BFCE是矩形.
∴BH=CH,
在△BEH和△CFH中
|
∴△BEH≌△CFH;
(2)解:当BH=EH时,四边形BFCE是矩形,
理由是:∵BH=CH,EH=FH,
∴四边形BFCE是平行四边形,
∵BH=CH,EH=FH,BH=EH,
∴BC=EF,
∴四边形BFCE是矩形.
点评:本题考查了全等三角形的性质和判定,平相似四边形的判定,矩形的判定的应用,主要考查学生的推理能力,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
下列说法中正确的是( )
| A、带根号的数都是无理数 |
| B、无限小数都是无理数 |
| C、无理数都是无限小数 |
| D、无理数就是开方开不尽的数 |
2008年9月27日,神舟七号航天员翟志刚完成中国历史上第一次太空行走,他相对地球行走了5 100千米路程,用科学记数法表示为( )
| A、51×102米 |
| B、5.1×103米 |
| C、5.1×106米 |
| D、0.51×107米 |
 如图,AB=CD,AD=CB,那么下列结论中错误的是( )
如图,AB=CD,AD=CB,那么下列结论中错误的是( )| A、∠A=∠C |
| B、AB=AD |
| C、AD∥BC |
| D、AB∥CD |
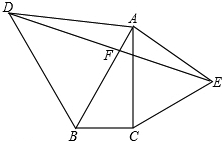 如图,在△ABC中,∠ABC=60°,分别以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接DE,交AB于点F,求证:DF=EF.
如图,在△ABC中,∠ABC=60°,分别以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接DE,交AB于点F,求证:DF=EF. 如图,已知AB=AE,BC=ED,AC=AD.
如图,已知AB=AE,BC=ED,AC=AD. 已知:如图,CE⊥AB,BF⊥AC,CE与BF相交于D,且BD=CD.求证:∠BAD=∠CAD.
已知:如图,CE⊥AB,BF⊥AC,CE与BF相交于D,且BD=CD.求证:∠BAD=∠CAD.