题目内容
19．求证：对于任意的正整数n，代数式n（n+7）-（n+3）（n-2）的值必然是6的倍数．分析 先将代数式化简合并，然后再因式分解，可得出一个含有6因式的式子，从而可作出判断．
解答 证明：∵n（n+7）-（n+3）（n-2）
=n2+7n-（n2+n-6）
=6n+6
=6（n+1），
∴当n为正整数时，6（n+1）总能被6整除，
即代数式n（n+7）-（n+3）（n-2）的值必然是6的倍数．．
点评 本题考查了整式的混合运算、数的整除性问题；难度不大，关键是得出化简后的式子，看因式中是否含有6或6的倍数．
练习册系列答案
相关题目
如图，AF为△ABC的平分线，以BC为直径的⊙0交AB于D，$\widehat{BE}=\widehat{DE}$，AF⊥CE，AB交CE于H．
如图，分别求一个或一组平移，使得：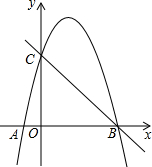
如图，抛物线y=ax2+bx-4a经过A（-1，0）、C（0，4）两点，与x轴交于另一点B．