题目内容
 已知,如图,过点A、O的圆与y轴相交于一点C,与AB相交于一点E,直线AB的解析式为y=kx+4k,过点A、O的抛物线y=ax2+bx+c的顶点为P.
已知,如图,过点A、O的圆与y轴相交于一点C,与AB相交于一点E,直线AB的解析式为y=kx+4k,过点A、O的抛物线y=ax2+bx+c的顶点为P.(1)若点C的坐标为(0,
| 4 |
| 3 |
| 3 |
(2)若AC=
| 2 |
分析:(1)因为直线AB的解析式为y=kx+4k,设y=0可得直线和x轴交点的坐标,利用锐角三角函数和已知条件可求出角BAO的度数,再解直角三角形ABO即可求出OB的长,进而求出B的坐标;
(2)利用有两对角相等的三角形相似可先证明△ACB∽△OEB,利用已知条件求出角BA0的度数,进一步得到三角形AOB是等腰直角三角形,进而得到直线的解析式,又因为抛物线的顶点坐标在P在直线上,可求出a的值,设任意一点M(x,y),能使(x+2)2+(y-2+m)2=(y-2-m)2成立,由抛物线的解析式和已知等式即可求出m的值.
(2)利用有两对角相等的三角形相似可先证明△ACB∽△OEB,利用已知条件求出角BA0的度数,进一步得到三角形AOB是等腰直角三角形,进而得到直线的解析式,又因为抛物线的顶点坐标在P在直线上,可求出a的值,设任意一点M(x,y),能使(x+2)2+(y-2+m)2=(y-2-m)2成立,由抛物线的解析式和已知等式即可求出m的值.
解答:解:(1)∵点C的坐标为(0,
),
∴OC=
,
∵直线AB的解析式为y=kx+4k,设y=0,
∴x=-4,
∴A的坐标为(-4,0),
∴AO=4,
∵tan∠CAO=
=
,
∴∠CAO=30°,
∵AC平分∠BAO,
∴∠BAO=60°,
∴BO=AO•tan60°=4×
=4
,
∴B(0,4
);
(2)∵∠B=∠B,∠BAC=∠BOE,
∴△ACB∽△OEB,
∴
=
,
∵AC=
OE,
∴
=
,
∵sin∠BAO=
=
,
∴∠BAO=45°,
∴AO=BO=4,
∴B坐标为(4,0)
把B坐标为(4,0)代入y=kx+4k得:k=1,
∴直线AB的解析式为y=x+4,
∵抛物线y=ax2+bx+c过点A、O,
∴可设y=a(x-0)(x+4)=a(x2+4x+4)-4a=a(x+2)2-4a,
∴顶点P的坐标为(-2,-4a),
∵顶点P在直线上,
∴-2+4=-4a,
∴a=-
,
∴y=-
(x+2)2+2,
设任意一点M(x,y),能使(x+2)2+(y-2+m)2=(y-2-m)2成立,
则(x+2)2=(y-2-m)2-(y-2+m)2成立,
∴(x+2)2=2(y-2)(-2m)
又∵y=-
(x+2)2+2,
∴(x+2)2=4-2y,
∴4-2y=-4my+8m,
∴4=8m,-2y=-4my,
∴m=
,
即存在m=
,对于抛物线y=-
(x+2)2+2上任意一点,都能使(x+2)2+(y-2+m)2=(y-2-m)2成立.
| 4 |
| 3 |
| 3 |
∴OC=
4
| ||
| 3 |
∵直线AB的解析式为y=kx+4k,设y=0,

∴x=-4,
∴A的坐标为(-4,0),
∴AO=4,
∵tan∠CAO=
| OC |
| AO |
| ||
| 3 |
∴∠CAO=30°,
∵AC平分∠BAO,
∴∠BAO=60°,
∴BO=AO•tan60°=4×
| 3 |
| 3 |
∴B(0,4
| 3 |
(2)∵∠B=∠B,∠BAC=∠BOE,
∴△ACB∽△OEB,
∴
| AC |
| EO |
| AB |
| BO |
∵AC=
| 2 |
∴
| BO |
| AB |
| ||
| 2 |
∵sin∠BAO=
| BO |
| AB |
| ||
| 2 |
∴∠BAO=45°,
∴AO=BO=4,
∴B坐标为(4,0)
把B坐标为(4,0)代入y=kx+4k得:k=1,
∴直线AB的解析式为y=x+4,
∵抛物线y=ax2+bx+c过点A、O,
∴可设y=a(x-0)(x+4)=a(x2+4x+4)-4a=a(x+2)2-4a,
∴顶点P的坐标为(-2,-4a),
∵顶点P在直线上,
∴-2+4=-4a,
∴a=-
| 1 |
| 2 |
∴y=-
| 1 |
| 2 |
设任意一点M(x,y),能使(x+2)2+(y-2+m)2=(y-2-m)2成立,
则(x+2)2=(y-2-m)2-(y-2+m)2成立,
∴(x+2)2=2(y-2)(-2m)
又∵y=-
| 1 |
| 2 |
∴(x+2)2=4-2y,
∴4-2y=-4my+8m,
∴4=8m,-2y=-4my,
∴m=
| 1 |
| 2 |
即存在m=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了一次函数和x轴交的问题、求二次函数得解析式、特殊角的三角函数、角平分线的定义、相似三角形的判定和性质以及存在性问题,题目的综合性很强,对学生灵活运用知识的能力要求很高.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 1、已知立方体如图,过点A与平面CB/平行的棱的条数有( )
1、已知立方体如图,过点A与平面CB/平行的棱的条数有( ) OAM关于x轴对称,其中A、B、C是过点P且垂直于x轴的直线与两弧及圆的交点,以点B为顶点且过点D的抛物线l交⊙P与另一点E.
OAM关于x轴对称,其中A、B、C是过点P且垂直于x轴的直线与两弧及圆的交点,以点B为顶点且过点D的抛物线l交⊙P与另一点E. 已知:如图,过点C(2,1)分别作x轴、y轴的平行线,交直线y=-x+4于B、A两点,若二次函数y=ax2+bx+c(a≠0)的图象经过坐标原点O,且顶点在矩形ADBC内(包括三边上),则a的取值范围是
已知:如图,过点C(2,1)分别作x轴、y轴的平行线,交直线y=-x+4于B、A两点,若二次函数y=ax2+bx+c(a≠0)的图象经过坐标原点O,且顶点在矩形ADBC内(包括三边上),则a的取值范围是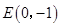 作平行于
作平行于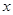 轴的直线
轴的直线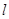 ,抛物线
,抛物线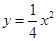 上的两点
上的两点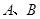 的横坐标分别为
的横坐标分别为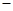 1和4,直线
1和4,直线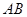 交
交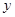 轴于点
轴于点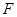 ,过点
,过点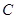 、
、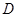 ,连接
,连接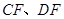 .
.
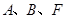 的坐标;
的坐标;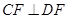 ;
;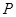 是抛物线
是抛物线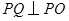 交
交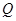 ,是否存在点
,是否存在点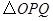 与
与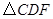 相似?若存在,请求出所有符合条件的点
相似?若存在,请求出所有符合条件的点