题目内容
 已知:如图,过点C(2,1)分别作x轴、y轴的平行线,交直线y=-x+4于B、A两点,若二次函数y=ax2+bx+c(a≠0)的图象经过坐标原点O,且顶点在矩形ADBC内(包括三边上),则a的取值范围是
已知:如图,过点C(2,1)分别作x轴、y轴的平行线,交直线y=-x+4于B、A两点,若二次函数y=ax2+bx+c(a≠0)的图象经过坐标原点O,且顶点在矩形ADBC内(包括三边上),则a的取值范围是-
≤a≤-
| 1 |
| 2 |
| 1 |
| 9 |
-
≤a≤-
.| 1 |
| 2 |
| 1 |
| 9 |
分析:由过点C(2,1)分别作x轴、y轴的平行线,交直线y=-x+4于B、A两点,即可求得点A与B的坐标,继而求得点D的坐标,又由二次函数y=ax2+bx+c(a≠0)的图象经过坐标原点O,且顶点在矩形ADBC内(包括三边上),可得a<0,然后由|a|越大,开口越小,可得当顶点在顶点在AC上时,a最小,当顶点在顶点在BD上时,a最大,继而求得答案.
解答:解:∵过点C(2,1)分别作x轴、y轴的平行线,交直线y=-x+4于B、A两点,
∴点A(2,2),点B(3,1),
∵四边形ABCD是矩形,
∴D(3,2),
∵二次函数顶点y=ax2+bx+c(a≠0)的图象经过坐标原点O,且在矩形ADBC内(包括三边上),
∴a<0,
∵|a|越大,开口越小,
即a越小,开口越小,
∴当顶点在顶点在AC上时,a最小,
设此时顶点坐标为(2,m),且1≤m≤2,
则二次函数的解析式为:y=a(x-2)2+m,
∵二次函数y=ax2+bx+c(a≠0)的图象经过坐标原点O,
∴a(0-2)2+m=0,
解得:a=-
,
∴当m=2时,a最小,a=-
;
∴当顶点在顶点在BD上时,a最大,
设此时顶点坐标为(3,n),且1≤n≤2,
则二次函数的解析式为:y=a(x-3)2+n,
∵二次函数y=ax2+bx+c(a≠0)的图象经过坐标原点O,
∴a(0-3)2+n=0,
解得:a=-
,
∴当m=1时,a最大,a=-
;
∴a的取值范围是:-
≤a≤-
.
故答案为:-
≤a≤-
.
∴点A(2,2),点B(3,1),
∵四边形ABCD是矩形,
∴D(3,2),
∵二次函数顶点y=ax2+bx+c(a≠0)的图象经过坐标原点O,且在矩形ADBC内(包括三边上),
∴a<0,
∵|a|越大,开口越小,
即a越小,开口越小,
∴当顶点在顶点在AC上时,a最小,
设此时顶点坐标为(2,m),且1≤m≤2,
则二次函数的解析式为:y=a(x-2)2+m,
∵二次函数y=ax2+bx+c(a≠0)的图象经过坐标原点O,
∴a(0-2)2+m=0,
解得:a=-
| m |
| 4 |
∴当m=2时,a最小,a=-
| 1 |
| 2 |
∴当顶点在顶点在BD上时,a最大,
设此时顶点坐标为(3,n),且1≤n≤2,
则二次函数的解析式为:y=a(x-3)2+n,
∵二次函数y=ax2+bx+c(a≠0)的图象经过坐标原点O,
∴a(0-3)2+n=0,
解得:a=-
| n |
| 9 |
∴当m=1时,a最大,a=-
| 1 |
| 9 |
∴a的取值范围是:-
| 1 |
| 2 |
| 1 |
| 9 |
故答案为:-
| 1 |
| 2 |
| 1 |
| 9 |
点评:此题考查了二次函数的性质、二次函数的解析式一般式与顶点式以及矩形的性质等知识.此题综合性较强,难度较大,注意掌握方程思想、分类讨论思想与数形结合思想的应用.

练习册系列答案
相关题目
 1、已知立方体如图,过点A与平面CB/平行的棱的条数有( )
1、已知立方体如图,过点A与平面CB/平行的棱的条数有( ) 已知,如图,过点A、O的圆与y轴相交于一点C,与AB相交于一点E,直线AB的解析式为y=kx+4k,过点A、O的抛物线y=ax2+bx+c的顶点为P.
已知,如图,过点A、O的圆与y轴相交于一点C,与AB相交于一点E,直线AB的解析式为y=kx+4k,过点A、O的抛物线y=ax2+bx+c的顶点为P. OAM关于x轴对称,其中A、B、C是过点P且垂直于x轴的直线与两弧及圆的交点,以点B为顶点且过点D的抛物线l交⊙P与另一点E.
OAM关于x轴对称,其中A、B、C是过点P且垂直于x轴的直线与两弧及圆的交点,以点B为顶点且过点D的抛物线l交⊙P与另一点E.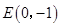 作平行于
作平行于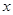 轴的直线
轴的直线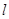 ,抛物线
,抛物线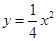 上的两点
上的两点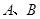 的横坐标分别为
的横坐标分别为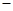 1和4,直线
1和4,直线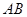 交
交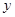 轴于点
轴于点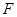 ,过点
,过点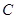 、
、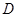 ,连接
,连接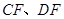 .
.
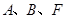 的坐标;
的坐标;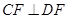 ;
;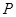 是抛物线
是抛物线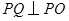 交
交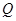 ,是否存在点
,是否存在点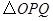 与
与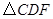 相似?若存在,请求出所有符合条件的点
相似?若存在,请求出所有符合条件的点