题目内容
 如图,已知等腰梯形ABCD中,AD∥BC,AC⊥BD,AD+BC=10,DE⊥BC于E.求DE的长.
如图,已知等腰梯形ABCD中,AD∥BC,AC⊥BD,AD+BC=10,DE⊥BC于E.求DE的长.
 解:过点D作DK∥AC,交BC的延长线于K,
解:过点D作DK∥AC,交BC的延长线于K,∵AD∥BC,
∴四边形ACKD是平行四边形,
∴CK=AD,AC=DK,
∵四边形ABCD是等腰梯形,
∴BD=AC=DK,
又∵DE⊥BC,
∴BE=KE(三线合一),
又∵DK∥AC,DE⊥BC,
∴∠BDK=90°,
∴DE=
 BK=
BK= (BC+CK)=
(BC+CK)= (BC+AD)=
(BC+AD)= ×10=5.
×10=5.分析:根据等腰梯形的性质,注意首先过点D作DK∥AC,交BC的延长线于K,即可得四边形ACKD是平行四边形,然后由直角三角形的性质,即可求得DE的长.
点评:本题考查等腰梯形的性质,有一定难度,注意掌握梯形面积的两种表示形式,从而解出梯形的高.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 ,
, 3、如图,已知等腰梯形ABCD中,AD∥BC,∠B=60°,AD=2,BC=8,则此等腰梯形的周长为( )
3、如图,已知等腰梯形ABCD中,AD∥BC,∠B=60°,AD=2,BC=8,则此等腰梯形的周长为( ) 如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC=
如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC= 13、如图,已知等腰梯形ABCD,AD∥BC,AD=5cm,BC=11cm,高DE=4cm,则梯形的周长为
13、如图,已知等腰梯形ABCD,AD∥BC,AD=5cm,BC=11cm,高DE=4cm,则梯形的周长为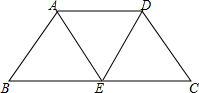 如图,已知等腰梯形ABCD是由三个边长为2的全等的正三角形围成的,则等腰梯形ABCD的面积是
如图,已知等腰梯形ABCD是由三个边长为2的全等的正三角形围成的,则等腰梯形ABCD的面积是