题目内容
3、如图，已知等腰梯形ABCD中，AD∥BC，∠B=60°，AD=2，BC=8，则此等腰梯形的周长为（ ）分析：作AE⊥BC，DF⊥BC，根据等腰梯形的性质求得BE，AB的长，从而再根据周长公式即可求得其周长．
解答：
解：如下图，作AE⊥BC，DF⊥BC，
∵AD=EF=2，又BE=CF
∴BE=CF=（8-2）÷2=3
∵∠B=60°，
∴∠BAE=30°，
∴AB=6
∵梯形ABCD是等腰梯形
∴AB=CD=6
∴周长为6+6+2+8=22，
故选D．
解：如下图，作AE⊥BC，DF⊥BC，∵AD=EF=2，又BE=CF
∴BE=CF=（8-2）÷2=3
∵∠B=60°，
∴∠BAE=30°，
∴AB=6
∵梯形ABCD是等腰梯形
∴AB=CD=6
∴周长为6+6+2+8=22，
故选D．
点评：等腰梯形的问题可以通过作高线转化为直角三角形的问题来解决．
练习册系列答案
相关题目
，
如图，已知等腰梯形ABCD中，AD∥BC，BD⊥DC，∠DBC=
13、如图，已知等腰梯形ABCD，AD∥BC，AD=5cm，BC=11cm，高DE=4cm，则梯形的周长为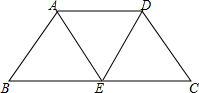
如图，已知等腰梯形ABCD是由三个边长为2的全等的正三角形围成的，则等腰梯形ABCD的面积是