题目内容
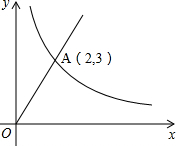 (2012•台州)如图,正比例函数y=kx(x≥0)与反比例函数y=
(2012•台州)如图,正比例函数y=kx(x≥0)与反比例函数y=| m | x |
(1)求k,m的值;
(2)写出正比例函数值大于反比例函数值时自变量x的取值范围.
分析:(1)将正比例函数与反比例函数图象的交点A的坐标代入正比例函数解析式中确定出k的值,代入反比例函数解析式中求出m的值;
(2)由两函数的交点A的横坐标为2,根据函数图象可得出当x大于2时,正比例函数图象在反比例函数图象上,即为正比例函数值大于反比例函数值时自变量x的取值范围.
(2)由两函数的交点A的横坐标为2,根据函数图象可得出当x大于2时,正比例函数图象在反比例函数图象上,即为正比例函数值大于反比例函数值时自变量x的取值范围.
解答:解:(1)把(2,3)代入y=kx得:3=2k,
∴k=
,
把(2,3)代入y=
得:3=
,
∴m=6;
(2)由图象可知,当正比例函数值大于反比例函数值时,
自变量x的取值范围是x>2.
∴k=
| 3 |
| 2 |
把(2,3)代入y=
| m |
| x |
| m |
| 2 |
∴m=6;
(2)由图象可知,当正比例函数值大于反比例函数值时,
自变量x的取值范围是x>2.
点评:此题考查了一次函数与反比例函数的交点问题,利用了数形结合的思想,两函数的交点即为两函数图象的公共点,此点满足两函数解析式.

练习册系列答案
相关题目
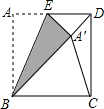 (2012•台州)如图,将正方形ABCD沿BE对折,使点A落在对角线BD上的A′处,连接A′C,则∠BA′C=
(2012•台州)如图,将正方形ABCD沿BE对折,使点A落在对角线BD上的A′处,连接A′C,则∠BA′C= (2012•台州)如图,为测量江两岸码头B、D之间的距离,从山坡上高度为50米的A处测得码头B的仰角∠EAB为15°,码头D的仰角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求码头B、D的距离(结果保留整数).
(2012•台州)如图,为测量江两岸码头B、D之间的距离,从山坡上高度为50米的A处测得码头B的仰角∠EAB为15°,码头D的仰角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求码头B、D的距离(结果保留整数). (2012•台州)如图,点D、E、F分别为△ABC三边的中点,若△DEF的周长为10,则△ABC的周长为( )
(2012•台州)如图,点D、E、F分别为△ABC三边的中点,若△DEF的周长为10,则△ABC的周长为( ) (2012•台州)如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
(2012•台州)如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )