题目内容
在△ABC中,∠BAC=90°,AD⊥BC于D,AB=3,AC=4,则AD=________.

分析:利用勾股定理求出BC,然后利用三角形的面积=
 AB×AC=
AB×AC= BC×AD可得出AD的长度.
BC×AD可得出AD的长度.解答:

由题意得,AB=3,AC=4,
在RT△ABC中,BC=
 =5,
=5,又∵S△ABC=
 AB×AC=
AB×AC= BC×AD,
BC×AD,∴AD=
 =
= .
.故答案为:

点评:本题考查了勾股定理,利用勾股定理求出BC的长是关键,另外要掌握本题利用面积的不同表示法求线段的长度的方法.

练习册系列答案
相关题目
 ;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.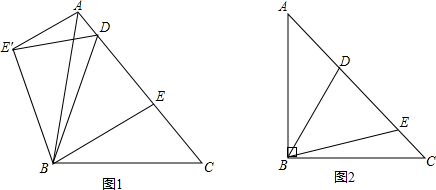
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.