题目内容
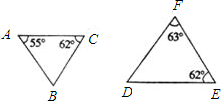
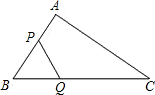
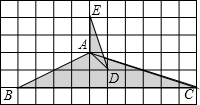
如图，点B、C、D在一条直线上，ED⊥CD，AC⊥EC，CB•CE=CA•ED．求证：△ABC∽△CDE．
证明：∵ED⊥CD，AC⊥EC，
∴∠ABC=∠EDC=90°，
∴∠ACB+∠ECD=90°，∠ECD+∠CED=∠90°，
∴∠ACB=∠CED，
又∵CB•CE=CA•ED，
∴
=
，
∴△ABC∽△CDE．
∴∠ABC=∠EDC=90°，
∴∠ACB+∠ECD=90°，∠ECD+∠CED=∠90°，
∴∠ACB=∠CED，
又∵CB•CE=CA•ED，
∴
| CA |
| CE |
| CB |
| ED |
∴△ABC∽△CDE．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
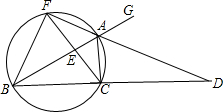的延长线相交于点D，延长DA与．△ABC的外接圆交于点F，连接FB、FC，FC与AB相交于点E．
