题目内容
7.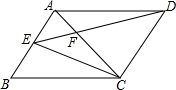 如图,已知点E为平行四边形ABCD中AB边上一点,且S△AEF=2,S△BEC=6,则S△EFC=4.
如图,已知点E为平行四边形ABCD中AB边上一点,且S△AEF=2,S△BEC=6,则S△EFC=4.
分析 由平行四边形的性质得出△ABC的面积=△CDE的面积,得出△AEF的面积+△BEC的面积=△CDF的面积=8,由平行线得出△AEF∽△CDF,由相似三角形面积的比等于相似比的平方求出$\frac{AF}{CF}$=$\frac{1}{2}$,得出S△EFC=2S△AEF=4即可.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥CD,△ABC的面积=$\frac{1}{2}$平行四边形ABCD的面积=△CDE的面积,
∴△AEF的面积+△BEC的面积=△CDF的面积,
即△CDF的面积=2+6=8,
∵AB∥CD,
∴△AEF∽△CDF,
∴$\frac{△AEF的面积}{△CDF的面积}=(\frac{AF}{CF})^{2}$=$\frac{2}{8}$=$\frac{1}{4}$,
∴$\frac{AF}{CF}$=$\frac{1}{2}$,
∴$\frac{△AEF的面积}{△EFC的面积}=\frac{AF}{CF}$=$\frac{1}{2}$,
∴S△EFC=2S△AEF=4;
故答案为:4.
点评 本题考查了平行四边形的性质、三角形面积的计算、相似三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形相似是解决问题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目