Question

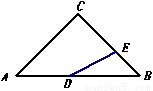
如图，在Rt中，∠C=90°，∠ABC=45°，AB=6，点D在AB边上，点E在BC边上（不与点B、C重合），且DA=DE，则AD的取值范围是           ．

 

Answer 1

【答案】

6－6≤AD＜3

【解析】

试题分析：以D为圆心，AD的长为半径画圆，当圆与BC相切时，AD最小，与线段BC相交且交点为B或C时，AD最大，分别求出即可得到范围．

以D为圆心，AD的长为半径画圆

①当圆与BC相切时，DE⊥BC时，

∵∠ABC=45°，

∴DE=BD，

∵AB=6，

∴设AD=DE=x，则DB=6-x，

∴ 

∴x=AD=6－6

②当圆与BC相交时，若交点为B或C，则AD=AB=3，

∴AD的取值范围是6－6≤AD＜3.

考点：等腰三角形的判定与性质

点评：利用边BC与圆的位置关系解答，分清AD最小和最大的两种情况是解决本题的关键．