题目内容
如图所示，直线L1⊥L2，垂足为点O，A，B是直线L1上的两点，且OB=2，AB=
．直线L1绕点O按逆时针方向旋转，旋转角度为a（0°＜a＜108°）．当a在什么范围内变化时，直线L2上存在点P，使得△BPA是以∠B为顶角的等腰三角形，请用不等式表示a的取值范围： ．
【答案】分析：△BPA是以∠B为顶角的等腰三角形，则需BP=AB．进一步求得点B到直线的最短距离及垂线段的长度，即可分析出旋转角的取值范围．
解答：
解：如图，作BC⊥L1于C点．
在△PBC中，BC＜BP．
∵BP=BA=
，
∴BC＜
，
∴cos∠OBC=
＜
，
∴∠OBC＞45°
而α=90°时两直线重合，
∴∠OBC≠90°，
∴45°≤α＜90°；
同理当l1旋转到l2的左边时∠OBC＜45°，
∴α=90°+∠OBC，
而0°＜a＜135°，
∴90°＜α＜135°，
所以45°≤α＜90°或90°＜α＜135°．
点评：此题注意分析出是等腰三角形应满足的条件，再进一步求得点B到直线的最短距离及垂线段的长度，即可分析出旋转角的取值范围．
解答：
解：如图，作BC⊥L1于C点．在△PBC中，BC＜BP．
∵BP=BA=
，∴BC＜
，∴cos∠OBC=
＜，∴∠OBC＞45°
而α=90°时两直线重合，
∴∠OBC≠90°，
∴45°≤α＜90°；
同理当l1旋转到l2的左边时∠OBC＜45°，
∴α=90°+∠OBC，
而0°＜a＜135°，
∴90°＜α＜135°，
所以45°≤α＜90°或90°＜α＜135°．
点评：此题注意分析出是等腰三角形应满足的条件，再进一步求得点B到直线的最短距离及垂线段的长度，即可分析出旋转角的取值范围．
练习册系列答案
相关题目
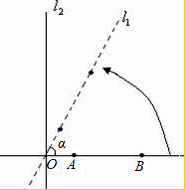如图所示，直线L1⊥L2，垂足为点O，A，B是直线L1上的两点，且OB=2，AB=
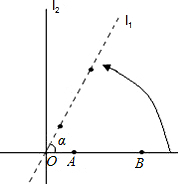角形，请用不等式表示α的取值范围：
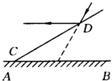44、如图所示，直线L1∥L2，C1，C2，C3是L1上的三点，连接C1A，C1B，C2A，C2B，C3A，C3B，得△C1AB，△C2AB，△C3AB，试说明△C1AB，△C2AB，△C3AB的面积相等．
2、如图所示，直线l1∥l2，∠1=40°，则∠2为（ ）