题目内容

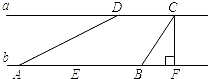
如图，∠ABC=∠BCD=90°，AC=15，cosA=
3
5
，BD=20，求S四边形ACDB的值．
在Rt△ABC中，∠ABC=90°
∵cosA=
AB
AC
，
∴AB=ACcosA=15×
3
5
=9；
∴BC=
AC2-AB2
=
152-92
=12，
在Rt△BCD中，∠BCD=90°
∵CD=
BD2-BC2
=
202-122
=16；
∴S四边形ACDB=
1
2
（AB+CD）•BC=
1
2
×（9+16）×12=150．
练习册系列答案
相关题目
如图，河流两岸a，b互相平行，C，D是河岸a上间隔50m的两个电线杆．某人在河岸b上的A处测得∠DAB=30°，然后沿河岸走了100m到达B处，测得∠CBF=60°，求河流的宽度CF的值．（结果精确到个位）
如图，某测量船位于海岛P的北偏西60°方向，距离海岛100海里的A处，它沿正南方向航行一段时间后，到达位于海岛P的西南方向上的B处，求测量船从A处航行到B处的路程（结果保留根号）．
如图，一束光线照在坡度为1：
3
的斜坡上，被斜坡上的平面镜反射成与地面平行的光线，则这束光线与坡面的夹角α是______度．
如图，CD是平面镜，光线从A点出发经CD上点E反射后照射到点B，若入射角为α（入射角等于反射角），AC⊥CD，BD⊥CD，垂足分别为C、D，且AC=3，CD=10，tanα=
4
3
，
（1）求CE的值；
（2）求BD的值？
已知A、B两点，如果A对B的俯角为α，那么B对A的仰角为（　　）
A．αB．90°-αC．90°+αD．180°-α
如图，在直角三角形ABC中，∠C=90°，D为斜边上一点，AD=2，BD=1，且四边形DECF是正方形，则图中阴影部分面积的和是______．
为了测量河对岸大树AB的高度，九年级（1）班数学兴趣小组设计了如图所示的测量方案，并得到如下数据：
（1）小明在大树底部点B的正对岸点C处，测得仰角∠ACB=30°；
（2）小红沿河岸测得DC=30米，∠BDC=45°．（点B、C、D在同一平面内，且CD⊥BC）
请你根据以上数据，求大树AB的高度．（结果保留一位小数）
（参考数据：
2
≈1.414，
3
≈1.732）
小山的顶部是一块平地，在这块平地上有一高压输电的铁架，小山的坡面坡度为1：
3
，斜坡BD的长是50米，在山坡的坡底B处测得铁架顶端A的仰角为45°，在山坡的坡顶D处测得铁架顶端A的仰角为60°．则小山的高度为______米，铁架的高度为______米（结果保留根号）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网