题目内容
解方程组 时,一学生把c看错得
时,一学生把c看错得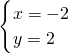 ,已知方程组的正确解是
,已知方程组的正确解是 ,则a,b,c的值是
,则a,b,c的值是
- A.a,b不能确定,c=-2
- B.a=4,b=5,c=-2
- C.a=4,b=7,c=-2
- D.a,b,c都不能确定
B
分析:是否看错了c值,并不影响两组解同时满足方程1,因此把这两组解代入方程1,可得到一个关于a、b的二元一次方程组,用适当的方法解得即可求出a、b.至于c,可把正确结果代入方程2,直接求解.
解答:把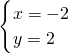 代入ax+by=2,得
代入ax+by=2,得
-2a+2b=2①,
把 代入方程组,得
代入方程组,得 ,
,
则①+②,得a=4.
把a=4代入①,得b=5.
由③,得c=-2.
∴a=4,b=5,c=-2.
故选B.
点评:注意理解方程组的解的定义,同时要正确理解题意,看错方程了,不是解错方程了.
分析:是否看错了c值,并不影响两组解同时满足方程1,因此把这两组解代入方程1,可得到一个关于a、b的二元一次方程组,用适当的方法解得即可求出a、b.至于c,可把正确结果代入方程2,直接求解.
解答:把
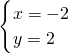 代入ax+by=2,得
代入ax+by=2,得-2a+2b=2①,
把
 代入方程组,得
代入方程组,得 ,
,则①+②,得a=4.
把a=4代入①,得b=5.
由③,得c=-2.
∴a=4,b=5,c=-2.
故选B.
点评:注意理解方程组的解的定义,同时要正确理解题意,看错方程了,不是解错方程了.

练习册系列答案
相关题目
解方程组 时,一学生把c看错得
时,一学生把c看错得 ,已知方程组的正确解是
,已知方程组的正确解是 ,则a、b、c的值是………………………( )
,则a、b、c的值是………………………( )
 时,一学生把c看错得
时,一学生把c看错得 ,已知方程组的正确解是
,已知方程组的正确解是 ,则a、b、c的值是………………………( )
,则a、b、c的值是………………………( )| A. a、b不能确定,c=-2 | B. a、b、c不能确定 |
| C. a=4,b=7,c=2 | D. a=4,b=5,c="-2" |
解方程组 时,一学生把c看错而得
时,一学生把c看错而得 而正确的解是
而正确的解是 那么 ( )
那么 ( )
 时,一学生把c看错而得
时,一学生把c看错而得 而正确的解是
而正确的解是 那么 ( )
那么 ( )| A.a、b、c的值不能确定 | B.a=4,b=5,c=-2 |
| C.a、b不能确定,c=-2 | D.a=4,b=7,c=2 |
 时,一学生把
时,一学生把 看错而得
看错而得 ,而正确的解是
,而正确的解是 那么
那么 、
、 、
、 时,一学生把c看错而得
时,一学生把c看错而得 而正确的解是
而正确的解是 那么
( )
那么
( )