题目内容
9．
如图，在平行四边形ABCD中，已知AD=7cm，AB=3cm，AE平分∠BAD交BC边于点E，则EC等于（ ）| A． | 1cm | B． | 2cm | C． | 3cm | D． | 4cm |
分析 根据平行四边形的性质和角平分线的性质可以推导出等角，进而得到等腰三角形，推得AB=BE，所以根据AD、AB的值，求出EC的值．
解答 解：∵AD∥BC，
∴∠DAE=∠BEA，
∵AE平分∠BAD，
∴∠BAE=∠DAE，
∴∠BAE=∠BEA，
∴BE=AB=3cm
∵BC=AD=7cm，
∴EC=BC-BE=7-3=4cm，
故选D．
点评 本题主要考查了平行四边形的性质，在平行四边形中，当出现角平分线时，一般可构造等腰三角形，进而利用等腰三角形的性质解题．
练习册系列答案
相关题目
19．在-5，0，3，-2这四个数中，绝对值最小的数是（ ）
| A． | -5 | B． | 0 | C． | 3 | D． | -2 |
17．$\frac{1}{2}$tan60°的值等于（ ）
| A． | 3 | B． | $\sqrt{3}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | $\frac{\sqrt{3}}{2}$ |
14．下列几何体中，主视图是矩形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
1．
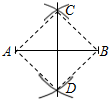老师在黑板上作线段AB的垂直平分线，步骤如下：分别以A、B为圆心，大于$\frac{1}{2}$AB的长为半径画弧，两弧相交于C、D，如图，根据他的作图方法可知四边形ADBC一定是（ ）
老师在黑板上作线段AB的垂直平分线，步骤如下：分别以A、B为圆心，大于$\frac{1}{2}$AB的长为半径画弧，两弧相交于C、D，如图，根据他的作图方法可知四边形ADBC一定是（ ）| A． | 矩形 | B． | 菱形 | C． | 正方形 | D． | 平行四边形 |
18．
如图是由6个棱长为1的正方体组成的几何体，其俯视图的面积是（ ）
如图是由6个棱长为1的正方体组成的几何体，其俯视图的面积是（ ）| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
19．计算（a3）2的结果为（ ）
| A． | a4 | B． | a5 | C． | a6 | D． | a7 |