题目内容
 在平行四边形ABCD中,对角线AC与BD相交于点O,若AC=6,BD=8,则边AB的取值范围是
在平行四边形ABCD中,对角线AC与BD相交于点O,若AC=6,BD=8,则边AB的取值范围是
- A.1<AB<7
- B.2<AB<1
- C.6<AB<8
- D.3<AB<4
A
分析:根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边.即可求解.本题可画出图形,再根据三角形形成的条件:任意两边之和大于第三边,任意两边之差小于第三边可得出AB的取值范围.
解答:∵四边形ABCD是平行四边形.
∴OA=3,OB=4.
在△AOB中:4-3<AB<4+3,即1<AB<7.故选A.
点评:本题考查的了平行四边形的性质和三角形的三边关系.平行四边形对角线互相平分.任意两边之和大于第三边,任意两边之差小于第三边.
分析:根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边.即可求解.本题可画出图形,再根据三角形形成的条件:任意两边之和大于第三边,任意两边之差小于第三边可得出AB的取值范围.
解答:∵四边形ABCD是平行四边形.
∴OA=3,OB=4.
在△AOB中:4-3<AB<4+3,即1<AB<7.故选A.
点评:本题考查的了平行四边形的性质和三角形的三边关系.平行四边形对角线互相平分.任意两边之和大于第三边,任意两边之差小于第三边.

练习册系列答案
相关题目
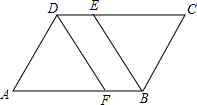 如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F.试判断AF与CE是否相等,并说明理由.
如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F.试判断AF与CE是否相等,并说明理由. 24、已知如图,在平行四边形ABCD中,BN=DM,BE=DF.求证:四边形MENF是平行四边形.
24、已知如图,在平行四边形ABCD中,BN=DM,BE=DF.求证:四边形MENF是平行四边形. (2013•鞍山一模)在平行四边形ABCD中,∠DAB=60°,点E是AD的中点,点O是AB边上一点,且AO=AE,过点E作直线HF交DC于点H,交BA的延长线于F,以OE所在直线为对称轴,△FEO经轴对称变换后得到△F′EO,直线EF′交直线DC于点M.
(2013•鞍山一模)在平行四边形ABCD中,∠DAB=60°,点E是AD的中点,点O是AB边上一点,且AO=AE,过点E作直线HF交DC于点H,交BA的延长线于F,以OE所在直线为对称轴,△FEO经轴对称变换后得到△F′EO,直线EF′交直线DC于点M. 如图,在平行四边形ABCD中,AE⊥AD交BD于点E,CF⊥BC交BD于点F.求证:BE=DF.
如图,在平行四边形ABCD中,AE⊥AD交BD于点E,CF⊥BC交BD于点F.求证:BE=DF. 如图,在平行四边形ABCD中,∠B的平分线交AD于E,AE=10,ED=4,那么平行四边形ABCD的周长是
如图,在平行四边形ABCD中,∠B的平分线交AD于E,AE=10,ED=4,那么平行四边形ABCD的周长是