题目内容
 如图,在四边形ABCD中,AD∥BC,点O在AD上,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=208°,求∠OBC+∠OCB的度数.请你将解答过程补充完整.
如图,在四边形ABCD中,AD∥BC,点O在AD上,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=208°,求∠OBC+∠OCB的度数.请你将解答过程补充完整.考点:平行线的性质
专题:
分析:根据两直线平行,同旁内角互补可得∠A+∠ABC=180°,∠D+∠DCB=180°,再根据角平分线的定义可得∠ABC=2∠OBC,∠DCB=2∠OCB,然后两式相加整理计算即可得解.
解答:解:∵AD∥BC,
∴∠A+∠ABC=180°,
∠D+∠DCB=180°,
∵BO,CO分别平分∠ABC,∠DCB,
∴∠ABC=2∠OBC,∠DCB=2∠OCB,
∴∠A+∠D+2(∠OBC+∠OCB)=360°,
∵∠A+∠D=208°,
∴∠OBC+∠OCB=76°.
∴∠A+∠ABC=180°,
∠D+∠DCB=180°,
∵BO,CO分别平分∠ABC,∠DCB,
∴∠ABC=2∠OBC,∠DCB=2∠OCB,
∴∠A+∠D+2(∠OBC+∠OCB)=360°,
∵∠A+∠D=208°,
∴∠OBC+∠OCB=76°.
点评:本题考查了平行线的性质,角平分线的定义,整体思想的利用是解题的关键.

练习册系列答案
相关题目
若|a-2013|+(b+1)2012=0,则b4的值为( )
| A、-1 | B、1 |
| C、-2013 | D、2013 |
下列运算正确的是( )
| A、a3×a2=a6 |
| B、(a3)3=a6 |
| C、a8÷a2=a6 |
| D、(a2b)3=a5b3 |
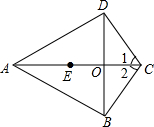 如图,在四边形ABCD中,AB=AD,BC=DC,AC、BD相交于点O,点E在AO上,且OE=OC.
如图,在四边形ABCD中,AB=AD,BC=DC,AC、BD相交于点O,点E在AO上,且OE=OC.
 如图,在8×8的正方形网格中,每个小正方形的边长均为1个单位,△ABC的三个顶点都在格点上.
如图,在8×8的正方形网格中,每个小正方形的边长均为1个单位,△ABC的三个顶点都在格点上.