Question

为了对一棵倾斜的古杉树AB进行保护，需测量其长度．如图，在地面上选取一点C，测得∠ACB=45°，AC=24m，∠BAC=66.5°，求这棵古杉树AB的长度．（结果取整数）

参考数据：≈1.41，sin66.5°≈0.92，cos66.5°≈0.40，tan66.5°≈2.30．

　

Answer 1

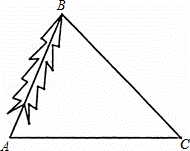
解：过B点作BD⊥AC于D．

∵∠ACB=45°，∠BAC=66.5°，

∴在Rt△ADB中，AD=，

在Rt△CDB中，CD=BD，

∵AC=AD+CD=24m，

∴+BD=24，

解得BD≈17m．

AB=≈18m．

故这棵古杉树AB的长度大约为18m．