Question

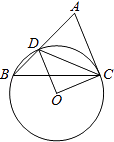
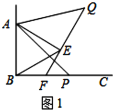
【题目】如图1，已知，是等边三角形，点为射线上任意一点（点与点不重合），连结，将线段绕点逆时针旋转得到线段，连结并延长交射线于点．

（1）如图1，当时，________，猜想________；

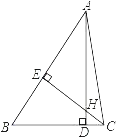
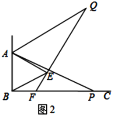
（2）如图2，当点为射线上任意一点时，猜想的度数，并说明理由；

Answer 1

【答案】（1），；（2），理由见解析

【解析】

（1）∠EBF与∠ABE互余，而∠ABE=60°，即可求得∠EBF的度数；先证明∠BAP=∠EAQ，进而得到△ABP≌△AEQ，证得∠AEQ=∠ABP=90°，则∠BEF=180°-∠AEQ-∠AEB=180°-90°-60°=30°，∠QFC=∠EBF+∠BEF，即可得到答案；

（2）先证明∠BAP=∠EAQ，进而得到△ABP≌△AEQ，证得∠AEQ=∠ABP=90°，则∠BEF=180°-∠AEQ-∠AEB=180°-90°-60°=30°，∠QFC=∠EBF+∠BEF，即可得到答案.

证明：（1）∵∠ABC=90°，△ABE是等边三角形，

∴∠ABE=60°，

∴∠EBF=30°；

猜想：；

理由如下：如图，

∵，，

∴，

∵，，

∴，

∴，

∴，

∴；

故答案为：30；60；

（2）结论：，

如图：

∵，

∴

在和中，，，

∴

∴．

∴

∴；