题目内容
【题目】y＝x2+（1﹣a）x+1是关于x的二次函数，当x的取值范围是1≤x≤3时，y在x＝1时取得最大值，则实数a的取值范围是（ ）
A. a≤﹣5B. a≥5C. a＝3D. a≥3
【答案】B
【解析】
由于二次函数的顶点坐标不能确定，故应分两种情况进行解答．
解：第一种情况：
当二次函数的对称轴不在1≤x≤3内时，此时，对称轴一定在1≤x≤3的右边，函数方能在这个区域取得最大值，
x＝
，即a≥7，
第二种情况：
当对称轴在1≤x≤3内时，对称轴一定是在区间1≤x≤3的中点的右边，因为如果在中点的左边的话，就是在x＝3的地方取得最大值，即： x＝
，即a≥5（此处若a取5的话，函数就在1和3的地方都取得最大值）
综合上所述a≥5．
故选：B．
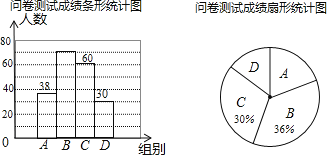
【题目】为了了解同学们对垃圾分类知识的了解程度，增强同学们的环保意识某校数学兴趣小组设计了“垃圾分类知识及投放情况”问卷，并在本校随机抽取若干名同学进行了问卷测试，根据测试成绩分布情况，将测试成绩分成A、B、C、D四组，绘制了如下统计图表
问卷测试成绩分组表
组别 | 分数/分 |
A | 60＜x≤70 |
B | 70＜x≤80 |
C | 80＜x≤90 |
D | 90＜x≤100 |
（1）本次抽样调查的样本总量是 ；
（2）样本中，测试成绩在B组的频数是 ，D组的频率是 ；
（3）样本中，这次测试成绩的中位数落在 组；
（4）如果该校共有880名学生，请估计成绩在90＜x≤100的学生约有 人．
【题目】某品牌手机去年每台的售价y（元）与月份x之间满足函数关系：y＝﹣50x+2600，去年的月销量p（万台）与月份x之间成一次函数关系，其中1﹣6月份的销售情况如下表：
月份（x） | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 |
销售量（p） | 3.9万台 | 4.0万台 | 4.1万台 | 4.2万台 | 4.3万台 | 4.4万台 |
（1）求p关于x的函数关系式；
（2）求该品牌手机在去年哪个月的销售金额最大？最大是多少万元？
（3）今年1月份该品牌手机的售价比去年12月份下降了m%，而销售量也比去年12月份下降了1.5m%．今年2月份，经销商决定对该手机以1月份价格的“八折”销售，这样2月份的销售量比今年1月份增加了1.5万台．若今年2月份这种品牌手机的销售额为6400万元，求m的值．
