题目内容
 如图,若△AOB≌△A′OB′,∠B=30°,∠AOA′=52°,则∠A′CO=
如图,若△AOB≌△A′OB′,∠B=30°,∠AOA′=52°,则∠A′CO=考点:全等三角形的性质
专题:
分析:根据全等三角形的性质得出∠B′=∠B=30°,∠AOB=∠A′OB′,求出∠AOA′=∠BOB′=52°,代入∠A′CO=∠B′+∠BOB′求出即可.
解答:解:∵△AOB≌△A′OB′,∠B=30°,
∴∠B′=∠B=30°,∠AOB=∠A′OB′,
∴∠AOB-∠A′OB=∠A′OB′-∠A′OB,
∴∠AOA′=∠BOB′=52°,
∴∠A′CO=∠B′+∠BOB′=30°+52°=82°,
故答案为:82°.
∴∠B′=∠B=30°,∠AOB=∠A′OB′,
∴∠AOB-∠A′OB=∠A′OB′-∠A′OB,
∴∠AOA′=∠BOB′=52°,
∴∠A′CO=∠B′+∠BOB′=30°+52°=82°,
故答案为:82°.
点评:本题考查了全等三角形的性质和三角形外角性质的应用,注意:全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
下列各组数中,互为相反数的一组是( )
A、2与
| |||
B、-2与
| |||
C、-2与
| |||
| D、|-3|与3 |
要组成一个三角形,三条线段长度可取( )
| A、3,4,8 |
| B、5,6,11 |
| C、2,2,3 |
| D、18,9,8 |
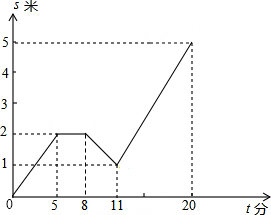 一个水池,装有一个进水管和一个出水管,两个水管同时开放,水池内水位高为S(单位:米)与注水时间t(单位:分)之间的函数关系图象如图所示,下列四种说法:
一个水池,装有一个进水管和一个出水管,两个水管同时开放,水池内水位高为S(单位:米)与注水时间t(单位:分)之间的函数关系图象如图所示,下列四种说法: