题目内容
如图,已知在Rt△ABC中,∠ACB=90°,BC>AC,⊙O为△ABC的外接圆,以点C为圆心,BC长为半径作弧交CA的延长线于点D,交⊙O于点E,连接BE、DE.(l)求∠DEB的度数;
(2)若直线DE交⊙0于点F,判断点F在半圆AB上的位置,并证明你的结论.

【答案】分析:(1)首先连接CE、BD,由圆周角定理可得:∠BDE= ∠ECB,∠DBE=
∠ECB,∠DBE= ∠ECD,则可求得∠BDE+∠DBE=45°,继而求得∠DEB的度数;
∠ECD,则可求得∠BDE+∠DBE=45°,继而求得∠DEB的度数;
(2)由(1)知∠DEB=135°,即可得∠BEF=45°,则可知弧FB= 弧AB;即F为弧AB中点.
弧AB;即F为弧AB中点.
解答: 解:(1)连接CE、BD,
解:(1)连接CE、BD,
∵∠BDE与∠ECB所对的弧都为弧EB,
∴∠BDE= ∠ECB,
∠ECB,
同理:∠DBE= ∠ECD,
∠ECD,
∴∠BDE+∠DBE= ∠DCB,
∠DCB,
∵∠ACB=90°,
∴∠BDE+∠DBE=45°,
 ∴∠DEB=180°-(∠BDE+∠DBE)=135°;
∴∠DEB=180°-(∠BDE+∠DBE)=135°;
(2)F为弧AB中点.
理由:连接BF,由(1)知∠DEB=135°,
∴∠ABF=45°,
∴ =
=
 ,
,
即F为弧AB中点.
点评:此题考查了圆周角定理以及弧与圆心角的关系.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.
 ∠ECB,∠DBE=
∠ECB,∠DBE= ∠ECD,则可求得∠BDE+∠DBE=45°,继而求得∠DEB的度数;
∠ECD,则可求得∠BDE+∠DBE=45°,继而求得∠DEB的度数;(2)由(1)知∠DEB=135°,即可得∠BEF=45°,则可知弧FB=
 弧AB;即F为弧AB中点.
弧AB;即F为弧AB中点.解答:
 解:(1)连接CE、BD,
解:(1)连接CE、BD,∵∠BDE与∠ECB所对的弧都为弧EB,
∴∠BDE=
 ∠ECB,
∠ECB,同理:∠DBE=
 ∠ECD,
∠ECD,∴∠BDE+∠DBE=
 ∠DCB,
∠DCB,∵∠ACB=90°,
∴∠BDE+∠DBE=45°,
 ∴∠DEB=180°-(∠BDE+∠DBE)=135°;
∴∠DEB=180°-(∠BDE+∠DBE)=135°;(2)F为弧AB中点.
理由:连接BF,由(1)知∠DEB=135°,
∴∠ABF=45°,
∴
 =
=
 ,
,即F为弧AB中点.
点评:此题考查了圆周角定理以及弧与圆心角的关系.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
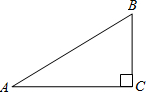 如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为( )
如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为( )| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
 (2012•驿城区模拟)如图,已知在Rt△ABC中,∠B=90°,D、E分别是边AB、AC的中点,若DE=4,AC=10,则AB的值为( )
(2012•驿城区模拟)如图,已知在Rt△ABC中,∠B=90°,D、E分别是边AB、AC的中点,若DE=4,AC=10,则AB的值为( ) 如图,已知在Rt△ABC中,∠C=90°,内切圆的半径为3cm,外接圆的半径为12.5cm,求△ABC的三边长.
如图,已知在Rt△ABC中,∠C=90°,内切圆的半径为3cm,外接圆的半径为12.5cm,求△ABC的三边长. 如图,已知在Rt△ABC中,∠C=90°,点D在BC上,AD=BD,sin∠ADC=
如图,已知在Rt△ABC中,∠C=90°,点D在BC上,AD=BD,sin∠ADC= 如图,已知在Rt△ABC中,∠C=90°.根据要求用尺规作图:
如图,已知在Rt△ABC中,∠C=90°.根据要求用尺规作图: