题目内容
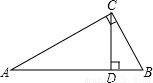
（2000•绍兴）如图，梯形ABCD中，AD∥BC，∠ABC=Rt∠，对角线AC⊥BD于P点．已知AD：BC=3：4，则BD：AC的值是（ ）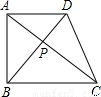
A．
B．
C．
D．
【答案】分析：由AD∥BC，可推△ADP∽△CBP，由相似三角形的性质可得
，所以AP=
AC，PC=
AC，BP=
BD，因∠ABC=90°，对角线AC⊥BD于P，利用△APB∽△BPC得到PB2=PA•PC，即可求解．
解答：解：∵AD∥BC
∴△ADP∽△CBP
∴
∴AP=
AC，PC=
AC，BP=
BD
∵∠ABC=90°，对角线AC⊥BD于P
∴△APB∽△BPC
∴PB2=PA•PC
∴
∴
．
故选A．
点评：本题需仔细分析题意，结合图形，利用相似三角形的性质即可解决问题．
，所以AP=AC，PC=AC，BP=BD，因∠ABC=90°，对角线AC⊥BD于P，利用△APB∽△BPC得到PB2=PA•PC，即可求解．解答：解：∵AD∥BC
∴△ADP∽△CBP
∴
∴AP=
AC，PC=AC，BP=BD∵∠ABC=90°，对角线AC⊥BD于P
∴△APB∽△BPC
∴PB2=PA•PC
∴
∴
．故选A．
点评：本题需仔细分析题意，结合图形，利用相似三角形的性质即可解决问题．
练习册系列答案
相关题目
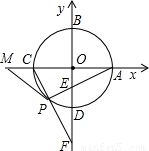
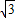，以线段OE，OF的长为根的一元二次方程为x2-
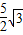x+m=0，求直线CF的解析式；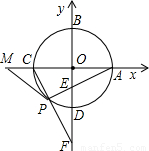
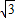，以线段OE，OF的长为根的一元二次方程为x2-
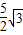x+m=0，求直线CF的解析式；
