题目内容
（2000•绍兴）如图，以OB为直径的半圆与半圆O交于点P，A、O、C、B在同一条直线上，作AD⊥AB与BP的延长线交于点D，若半圆O的半径为2，∠D的余弦值是方程3x2-10x+3=0的根，则AB的长等于（ ）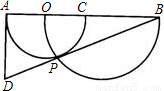
A．
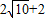
B．
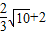
C．8
D．5
【答案】分析：根据方程3x2-10x+3=0求得其两个根，再设AD=x，BD=3x，则可用式子表示出AB，BC，列方程即可求得AB的长．
解答：解：∵3x2-10x+3=0，
∴x=3（不合题意，舍去）或x=
．
∴cosD=AD：BD=1：3，
设AD=x，则BD=3x．
∴AB=
=2
x，BC=2
x-4．
∴（2x）2=（2
x-4）•
x．
∴x=0（舍去），或x=2
．
∴AB=2
×2
=8．
故选C．
点评：此题考查圆的切线长定理，切割线定理、勾股定理等知识的综合运用．
解答：解：∵3x2-10x+3=0，
∴x=3（不合题意，舍去）或x=
．∴cosD=AD：BD=1：3，
设AD=x，则BD=3x．
∴AB=
=2x，BC=2x-4．∴（2x）2=（2
x-4）•x．∴x=0（舍去），或x=2
．∴AB=2
×2=8．故选C．
点评：此题考查圆的切线长定理，切割线定理、勾股定理等知识的综合运用．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
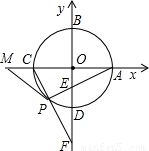
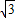，以线段OE，OF的长为根的一元二次方程为x2-
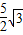x+m=0，求直线CF的解析式；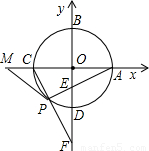
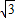，以线段OE，OF的长为根的一元二次方程为x2-
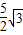x+m=0，求直线CF的解析式；
