Question

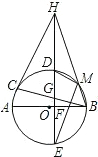
在等腰梯形ABCD中，AD∥BC，AB=DC，且BC=2．以CD为直径作⊙O′交AD于点E，过点E作EF⊥AB于点F．建立如图所示的平面直角坐标系，已知A、B两点坐标分别为A（2，0）、B（0，2

3

）．
（1）求C、D两点的坐标；
（2）求证：EF为⊙O′的切线；
（3）将梯形ABCD绕点A旋转180°到A′B′C′D′，直线CD上是否存在点P，使以点P为圆心，PD为半径的⊙P与直线C′D′相切？如果存在，请求出P点坐标；如果不存在，请说明理由．

Answer 1

（1）连接CE，如图，
∵CD是⊙O′的直径，
∴CE⊥x轴，
∵四边形ABCD为等腰梯形ABCD，
∵EO=BC=2，
CE=BO=2

3

，
DE=AO=2
∴DO=4，
∴C（-2，2

3

）D（-4，0）；

（2）证明：连接O′E，如图，在⊙O′中，
∵O′D=O′E，
∴∠O′DE=∠1，
在等腰梯形ABCD中，∠CDA=∠BAD
∴∠1=∠BAD
∴O′E∥BA
又∵EF⊥BA
∴O′E⊥EF
∴EF为⊙O′的切线．

（3）存在．理由如下：
过A作AM⊥CD于M，且交C′D′于N
∵梯形A′B′C′D′与梯形ABCD关于点A成中心对称
∴C′D′∥CD，
∴AN⊥C′D′且AM=AN，
在Rt△CDE中，CE=2

3

，DE=2，
∴∠D=60°
在Rt△ADM中，
AM=AD•sinD=[2-（-4）]•sin60°=3

3

，
∴MN=6

3

．
设点P存在，则PD=MN=6

3

，
作PQ⊥x轴于点Q，
∴PQ=PD•sinD=6

3

•

3

2

=9，
DQ=PD•cosD=6

3

•

1

2

=3

3

，
①若点P在DC的延长线上，
∴OQ=DQ-DO=3

3

-4，
∴P（3

3

-4，9）．
②若点P在CD的延长线上，
∴OQ=3

3

+4，
∴P（-3

3

-4，-9）．
∴在直线CD上存在点P（3

3

-4，9）和P（-3

3

-4，-9），使以点P为圆心，PD为半径的⊙P与直线C′D′相切．