题目内容
如图，AC=BC，AD=BD，MN分别是AC，BC中点，请问：DM=DN吗？请说明理由．分析：连接CD，利用sss即可证得△ACD≌△BCD，证得∠ACD=∠BCD，再根据SAS即可证得：△CMD≌△CND，则DM=DN．
解答：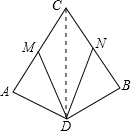
证明：连接CD．
∵点M和N分别是AC和BC的中点，AC=BC，
∴CM=CN．
在△ACD和△BCD中，
∵
，
∴△ACD≌△BCD（SSS），
∴∠ACD=∠BCD，
在△CMD和△CND中，
∵
，
∴△CMD≌△CND（SAS），
∴DM=DN．
证明：连接CD．∵点M和N分别是AC和BC的中点，AC=BC，
∴CM=CN．
在△ACD和△BCD中，
∵
|
∴△ACD≌△BCD（SSS），
∴∠ACD=∠BCD，
在△CMD和△CND中，
∵
|
∴△CMD≌△CND（SAS），
∴DM=DN．
点评：本题考查了全等三角形的判定与性质，证明线段相等的问题转化为证明三角形全等是常用的方法，本题解决的关键是正确作出辅助线，构造三角形．
练习册系列答案
相关题目
如图，AC⊥BC，AD⊥BD，AD=BC，CE⊥AB，DF⊥AB，垂足分别是E，F，那么，CE=DF吗？
已知，如图，AC=BC，AD=BD，下列结论中不正确的是（ ）
如图，AC⊥BC，DE是AB的垂直平分线，∠CAE=30°，则∠B=
如图，AC⊥BC，AD=BD，为了使图中的△BCD是等边三角形，再增加一个条件可以是（ ）
已知如图：AC⊥BC，CD⊥AB，则点B到AC的距离是线段