题目内容
若a、b、c为一个三角形的三边,则代数式(a-c)2-b2的值为
- A.一定为正数
- B.一定为负数
- C.可能为正数,也可能为负数
- D.可能为零
B
分析:根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边.即可求解.
解答:首先运用因式分解,得:原式=(a-c+b)(a-c-b).
再根据三角形的三边关系:两边之和大于第三边,两边之差小于第三边.
即a-c+b>0,a-c-b<0,两数相乘,异号得负,故代数式的值小于0.
故选B.
点评:本题利用了三角形中三边的关系:在三角形中,任意两边之和>第三边,任意两边之差<第三边.
分析:根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边.即可求解.
解答:首先运用因式分解,得:原式=(a-c+b)(a-c-b).
再根据三角形的三边关系:两边之和大于第三边,两边之差小于第三边.
即a-c+b>0,a-c-b<0,两数相乘,异号得负,故代数式的值小于0.
故选B.
点评:本题利用了三角形中三边的关系:在三角形中,任意两边之和>第三边,任意两边之差<第三边.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
若a、b、c为一个三角形的三条边,则代数式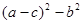 的值( )
的值( )
| A.一定为正数 | B.一定为负数 |
| C.可能为正数,也可能为负数 | D.可能为零 |
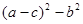 的值( )
的值( ) 表示一个一位数,
表示一个一位数, 表示一个两位数,若把
表示一个两位数,若把 B.
B. C.
C. D.
D.
 表示一个一位数,
表示一个一位数, 表示一个两位数,若把
表示一个两位数,若把 B.
B. C.
C. D.
D.